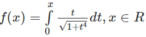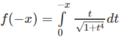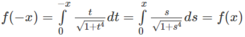Các câu hỏi tương tự
Chứng minh rằng hàm số f(x) cho bởi
f
x
∫
0
x
t
1
+
t
4
dt
,
x
∈
R
là hàm s...
Đọc tiếp
Chứng minh rằng hàm số f(x) cho bởi f x = ∫ 0 x t 1 + t 4 dt , x ∈ R là hàm số chẵn.
Giả sử hàm số f(x) liên tục trên đoạn [-a; a]. Chứng minh rằng:(1) : nếu f là hàm số chẵn(2): nếu f là hàm số lẻ.Áp dụng để tính:
Đọc tiếp
Giả sử hàm số f(x) liên tục trên đoạn [-a; a]. Chứng minh rằng:
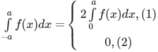
(1) : nếu f là hàm số chẵn
(2): nếu f là hàm số lẻ.
Áp dụng để tính:
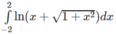
Giả sử hàm số f(x) liên tục trên đoạn [-a; a]. Chứng minh rằng:
∫
-
a
a
f
x
d
x
2
∫
0
a...
Đọc tiếp
Giả sử hàm số f(x) liên tục trên đoạn [-a; a]. Chứng minh rằng:
∫ - a a f x d x = 2 ∫ 0 a f x d x 1 0 2
(1) : nếu f là hàm số chẵn
(2): nếu f là hàm số lẻ.
Áp dụng để tính: ∫ - 2 2 ln x + 1 + x 2 d x
Chứng minh rằng các hàm số F(x) và G(x) sau đều là một nguyên hàm của cùng một hàm số:
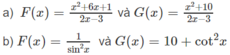
Chứng minh rằng các hàm số F(x) và G(x) sau đều là một nguyên hàm của cùng một hàm số: F x = 1 sin 2 x và G x = 10 + cot 2 x
Giả sử f(x) là hàm số liên tục trên đoạn [a; b], F(x) và G(x) là hai nguyên hàm của f(x). Chứng minh rằng F(b) – F(a) = G(b) – G(a), (tức là hiệu số F(b) – F(a) không phụ thuộc việc chọn nguyên hàm).
Chứng minh rằng các hàm số F(x) và G(x) sau đều là một nguyên hàm của cùng một hàm số:
F
x
x
2
+
6
x
+
1
2
x
-
3...
Đọc tiếp
Chứng minh rằng các hàm số F(x) và G(x) sau đều là một nguyên hàm của cùng một hàm số: F x = x 2 + 6 x + 1 2 x - 3 và G x = x 2 + 10 2 x - 3
Giả sử hàm số f(x) liên tục trên đoạn [a; b]. Chứng minh rằng:
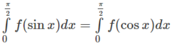
Giả sử hàm số f(x) liên tục trên đoạn [a; b]. Chứng minh rằng:
∫
0
π
2
f
sinx
d
x
∫
0
π
2
f
cosx...
Đọc tiếp
Giả sử hàm số f(x) liên tục trên đoạn [a; b]. Chứng minh rằng: ∫ 0 π 2 f sinx d x = ∫ 0 π 2 f cosx d x