Cho hàm số y = - x 3 - 3 x 2 + 9 x + 1 xác định trên R. Bảng biến thiên của hàm số là bảng nào trong các bảng biến thiên dưới đây?
A. 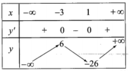
B. 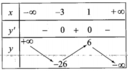
C. 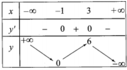
D. 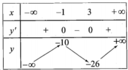
Cho hàm số y=f(x) có đạo hàm f'(x)= x ( x - 1 ) 2 ( x 2 + m x + 9 ) . Có bao nhiêu số nguyên dương m để hàm số y=f(3-x) đồng biến trên khoảng ( 3 ; + ∞ ) .
A. 6.
B. 8.
C. 5.
D. 7.
Hàm số nào sau đây là hàm số bậc hai?
a) \(y = 9{x^2} + 5x + 4\)
b) \(y = 3{x^3} + 2x + 1\)
c) \(y = - 4{(x + 2)^3} + 2(2{x^3} + 1) + x + 4\)
d) \(y = 5{x^2} + \sqrt x + 2\)
Hàm số ở câu a) \(y = 9{x^2} + 5x + 4\) là hàm số bậc hai với \(a = 9,b = 5,c = 4\)
Hàm số ở câu b), c) không phải là hàm số bậc hai vì chứa \({x^3}\)
Hàm số ở câu d) \(y = 5{x^2} + \sqrt x + 2\) không phải là hàm số bậc hai vì chứa \(\sqrt x \)
1) đạo hàm của hàm số \(y=x^2-3\sqrt{x}+\dfrac{1}{x}\)
2) đạo hàm của hàm số \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt{x}\) tại điểm x = 1
1) \(y=x^2-3\sqrt[]{x}+\dfrac{1}{x}\)
\(\Rightarrow y=2x-\dfrac{3}{2\sqrt[]{x}}-\dfrac{1}{x^2}\)
2) \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt[]{x}\)
\(\Rightarrow f'\left(x\right)=\dfrac{1.\left(x+3\right)-1\left(x+9\right)}{\left(x+3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=\dfrac{x+3-x-9}{\left(x+3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=\dfrac{-6}{\left(x+3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(1\right)=\dfrac{-6}{\left(1+3\right)^2}+\dfrac{2}{\sqrt[]{1}}=-\dfrac{3}{8}+2=\dfrac{13}{8}\)
1. đạo hàm của hàm số f(x) = 2x - 5 tại \(x_0=4\)
2. đạo hàm của hàm số \(y=x^2-3\sqrt{x}+\dfrac{1}{x}\)
3. đạo hàm của hàm số \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt{x}\) tại điểm x = 1
1) \(f\left(x\right)=2x-5\)
\(f'\left(x\right)=2\)
\(\Rightarrow f'\left(4\right)=2\)
2) \(y=x^2-3\sqrt[]{x}+\dfrac{1}{x}\)
\(\Rightarrow y'=2x-\dfrac{3}{2\sqrt[]{x}}-\dfrac{1}{x^2}\)
3) \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt[]{x}\)
\(\Rightarrow f'\left(x\right)=\dfrac{1.\left(x+3\right)-1.\left(x+9\right)}{\left(x-3\right)^2}+\dfrac{4}{2\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=\dfrac{x+3-x-9}{\left(x-3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=\dfrac{12}{\left(x-3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=2\left[\dfrac{6}{\left(x-3\right)^2}+\dfrac{1}{\sqrt[]{x}}\right]\)
\(\Rightarrow f'\left(1\right)=2\left[\dfrac{6}{\left(1-3\right)^2}+\dfrac{1}{\sqrt[]{1}}\right]=2\left(\dfrac{3}{2}+1\right)=2.\dfrac{5}{2}=5\)
Cho hàm số y= f( x) có đạo hàm f ' ( x ) = x 2 ( x - 9 ) ( x - 4 ) 2 . Xét hàm số y= g( x) =f( x2) Trong các phát biểu sau; tìm số phát biểu đúng
I. Hàm số y = g( x) đồng biến trên( 3; +∞)
II. Hàm số y= g(x) nghịch biến trên( -∞; -3)
III. Hàm số y= g( x) có 5 điểm cực trị
IV. m i n x ∈ R g ( x ) = f ( 9 )
A. 1
B. 2
C. 3
D. 4
Ta có
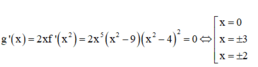
Bảng biến thiên của hàm số y= g( x)
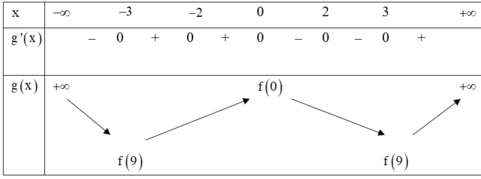
Dựa vào bảng biến thiên ta thấy hàm số đồng biến trên khoảng ( 3: + ∞) hàm số nghịch biến trong khoảng (-∞; -3) .
Hàm số có 3 cực trị, hàm số đạt giá trị nhỏ nhất tại x= ±3
Vậy có 3 khẳng định đúng là khẳng định I, II, IV
Chọn C.
Bài 1. Cho hàm số y= f(x)= {-2(x2 + 1) khi x ≤ 1 Tính f(1);f(2),f(√2 phần 2);f(√2)
{4√x-1 khi x > 1
Bài 2.Cho hàm số y= f(x)= { √-3x+8 khi x < 2 Tính f(-3);f(2);f(1),f(9)
{√x+7 khi x ≥ 2
Ở góc trái khung soạn thảo có hỗ trợ viết công thức toán (biểu tượng $\sum$). Bạn viết lại đề bằng cách này để được hỗ trợ tốt hơn.
TÌM GTNN CỦA HÀM SỐ SAU:
a) y=\(\dfrac{x^2+x+2}{\sqrt{x^2+x+1}}\)
TÌM GTLN CỦA HÀM SỐ SAU:
b)y= \(x^2\sqrt{9-x^2}với-3\le x\le3\)
c)y=\(\left(1-x\right)^3\left(1+3x\right)với\dfrac{-1}{3}\le x\le1\)
\(a,\dfrac{x^2+x+2}{\sqrt{x^2+x+1}}=\dfrac{x^2+x+1+1}{\sqrt{x^2+x+1}}=\sqrt{x^2+x+1}+\dfrac{1}{\sqrt{x^2+x+1}}\left(1\right)\)
Áp dụng BĐT cosi: \(\left(1\right)\ge2\sqrt{\sqrt{x^2+x+1}\cdot\dfrac{1}{\sqrt{x^2+x+1}}}=2\)
Dấu \("="\Leftrightarrow x^2+x+1=1\Leftrightarrow x^2+x=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)
Mọi người giúp mk câu này vs ạ
Bài 8. Cho hàm số y = f(x) = x -2
a)Tính f(-1) ; f(0)
b)Tìm x để f(x) = 3
c)Điểm nào sau đây thuộc đồ thị của hàm số y = f(x) = x -2 : A(1;0) ; B(-1;-3) C(3;-1)
Bài 9. a) Vẽ đồ thị của hàm số y = - 2x
b) Điểm sau điểm nào thuộc đồ thị hàm số: A (-2; 4); B(-1; -2)
Bài 10: Cho hàm số y = f(x) = ax (a # 0)
a)Tìm a biết đồ thị hàm số đi qua điểm A( 1; -3)
b)Vẽ đồ thị ứng với giá trị a vừa tìm được
Bài 8:
a) f(-1) = (-1) - 2 = -3
f(0) = 0 - 2 = -2
b) f(x) = 3
\(\Rightarrow x-2=3\)
\(x=3+2\)
\(x=5\)
Vậy \(x=5\) thì f(x) = 3
c) Thay tọa độ điểm A(1; 0) vào hàm số, ta có:
VT = 0; VP = 1 - 2 = -1
\(\Rightarrow VT\ne VP\)
\(\Rightarrow\) Điểm A(1; 0) không thuộc đồ thị của hàm số đã cho
Thay tọa độ điểm B(-1; -3) vào hàm số, ta có:
VT = -3; VP = -1 - 2 = -3
\(\Rightarrow VT=VP=-3\)
\(\Rightarrow\) Điểm B(-1; -3) thuộc đồ thị hàm số đã cho
Thay tọa độ điểm C(3; -1) vào hàm số, ta có:
VT = -1; VP = 3 - 2 = 1
\(\Rightarrow VT\ne VP\)
\(\Rightarrow\) Điểm C(3; -1) không thuộc đồ thị hàm số đã cho.
Bài 8:
a. y = f(x) = -1- 2= -3
y = f(x) = 0-2= -2
b. cho y = f(x)= 3
ta có: 3=x-2 => x-2=3
x= 3+2
x= 5
c. điểm B
Cho hàm số y = f ( x ) có đạo hàm f ' ( x ) = ( x - 2 ) ( x 2 - 3 ) ( x 4 - 9 ) . Số điểm cực trị của hàm số y = f ( x ) là
A. 3
B. 4
C. 2
D. 1
Bài 1: Xét tính đơn điệu của hàm số \(y=f(x)\) khi biết đạo hàm của hàm số là:
a) \(f'(x)=(x+1)(1-x^2)(2x-1)^3\)
b) \(f'(x)=(x+2)(x-3)^2(x-4)^3\)
Bài 2: Cho hàm số \(y=f(x)\) có đạo hàm \(f'(x)=x(x+1)(x-2)\). Xét tính biến thiên của hàm số:
a) \(y=f(2-3x)\)
b) \(y=f(x^2+1)\)
c) \(y=f(3x+1)\)