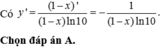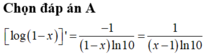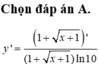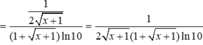Tình đạo hàm của các hàm số y = log 1 3 x - 4 x + 4
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
PB
Những câu hỏi liên quan
Tính đạo hàm của các hàm số sau:
a) \(y = \left( {{x^2} + 3x - 1} \right){e^x}\);
b) \(y = {x^3}{\log _2}x\).
a: \(y'=\left(x^2+3x-1\right)'\cdot e^x+\left(x^2+3x-1\right)\cdot\left(e^x\right)'\)
\(=e^x\left(2x+3\right)+\left(x^2+3x-1\right)\cdot e^x\)
\(=e^x\left(x^2+5x+2\right)\)
b: \(y'=\left(x^3\right)'\cdot log_2x+x^3\cdot\left(log_2x\right)'\)
\(=3x^2\cdot log_2x+x^3\cdot\dfrac{1}{x\cdot ln2}\)
Đúng 1
Bình luận (0)
Tính đạo hàm của các hàm số sau:
a) \(y = x{\log _2}x\);
b) \(y = {x^3}{e^x}\).
a: \(y'=\left(x\cdot log_2x\right)'=log_2x+x\cdot\dfrac{1}{x\cdot ln2}=log_2x+\dfrac{1}{ln2}\)
b: \(y'=\left(x^3e^x\right)'=\left(x^3\right)'\cdot e^x+x^3\cdot\left(e^x\right)'\)
\(=3x^2\cdot e^x+x^3\cdot e^x\)
Đúng 0
Bình luận (0)
Tính đạo hàm của các hàm số sau:
a) \(y = {2^{3x - {x^2}}};\)
b) \(y = {\log _3}\left( {4x + 1} \right).\)
tham khảo:
a)y′=2\(^{3x-x^2}\).ln2.(3−2x)
b) y′\(\dfrac{4}{ln3}\).\(\dfrac{1}{4x+1}\).4=\(\dfrac{4}{\left(4x+1\right)ln3}\)
Đúng 1
Bình luận (0)
Đạo hàm của hàm số
y
log
(
1
-
x
)
bằng A.
1
(
x
-
1
)
ln
10
B.
1
x
-
1
C.
1
1
-
x...
Đọc tiếp
Đạo hàm của hàm số y = log ( 1 - x ) bằng
A. 1 ( x - 1 ) ln 10
B. 1 x - 1
C. 1 1 - x
D. - 1 ( x - 1 ) ln 10
Đạo hàm của hàm số ylog(1-x) là A.
1
x
-
1
ln
10
B.
1
1
-
x
C.
1...
Đọc tiếp
Đạo hàm của hàm số y=log(1-x) là
A. 1 x - 1 ln 10
B. 1 1 - x
C. 1 1 - x ln 10
D. 1 x - 1
Đạo hàm của hàm số y= log(1 - x) bằng
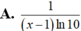
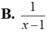
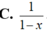
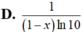
Đạo hàm của hàm số y=log(1-x) là
![]()
![]()

Đạo hàm của hàm số
y
log
(
1
+
x
+
1
)
là A. B. C. D.
Đọc tiếp
Đạo hàm của hàm số y = log ( 1 + x + 1 ) là
A. 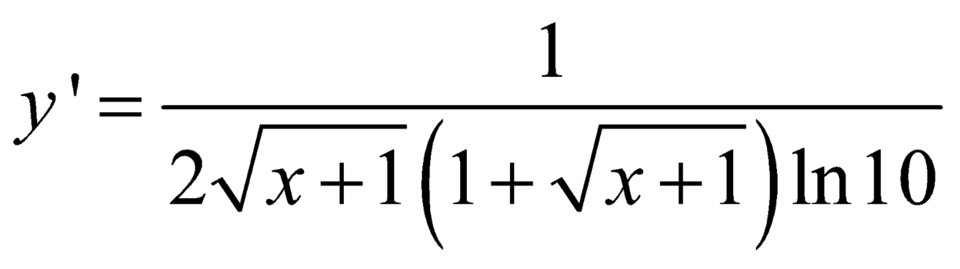
B. 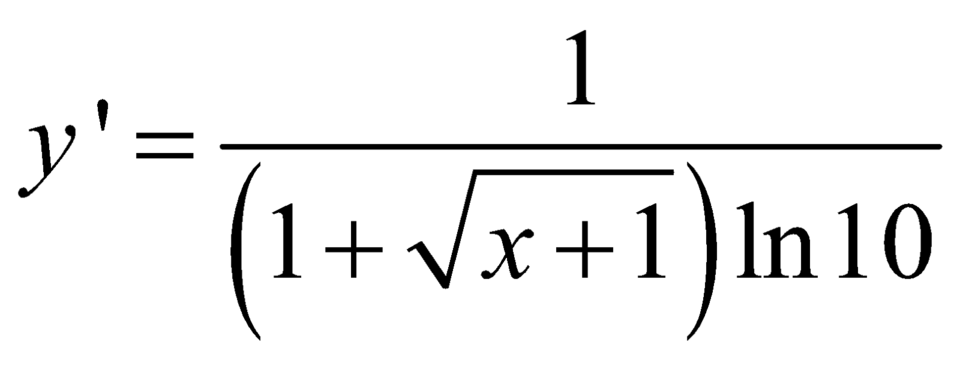
C. 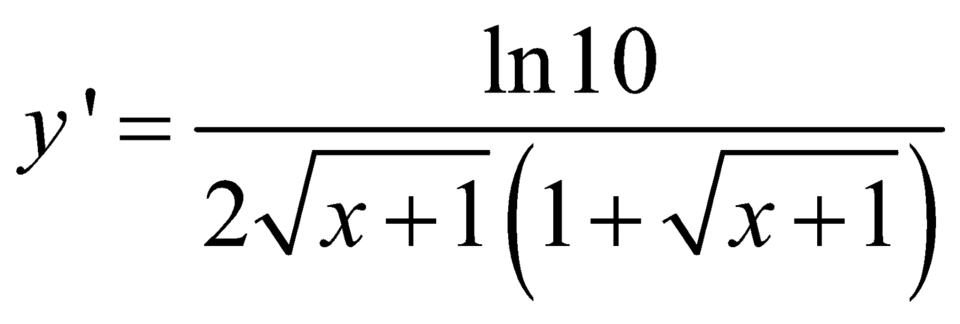
D. 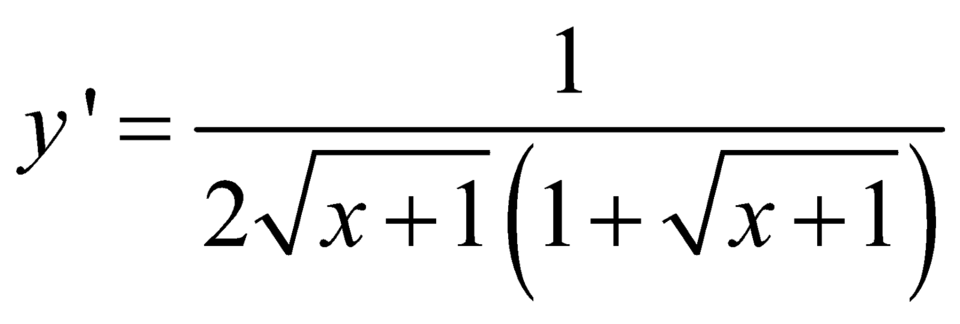
Tính đạo hàm của các hàm số sau:
a) \(y = \left( {{x^2} - x} \right){.2^x}\);
b) \(y = {x^2}{\log _3}x\);
c) \(y = {e^{3x + 1}}\).
a) \(y' = {\left( {{x^2} - x} \right)^\prime }{.2^x} + \left( {{x^2} - x} \right).{\left( {{2^x}} \right)^\prime } = \left( {2{\rm{x}} - 1} \right){.2^x} + \left( {{x^2} - x} \right){.2^x}.\ln 2\).
b) \(y' = {\left( {{x^2}} \right)^\prime }.{\log _3}x + {x^2}.{\left( {{{\log }_3}x} \right)^\prime } = 2{\rm{x}}.{\log _3}x + {x^2}.\frac{1}{{x\ln 3}} = 2{\rm{x}}.{\log _3}x + \frac{x}{{\ln 3}}\).
c) Đặt \(u = 3{\rm{x}} + 1\) thì \(y = {e^u}\). Ta có: \(u{'_x} = {\left( {3{\rm{x}} + 1} \right)^\prime } = 3\) và \(y{'_u} = {\left( {{e^u}} \right)^\prime } = {e^u}\).
Suy ra \(y{'_x} = y{'_u}.u{'_x} = {e^u}.3 = 3{{\rm{e}}^{3{\rm{x}} + 1}}\).
Vậy \(y' = 3{{\rm{e}}^{3{\rm{x}} + 1}}\).
Đúng 0
Bình luận (0)
Tính đạo hàm của các hàm số sau:
a) \(y = {\left( {2{x^3} + 3} \right)^2}\);
b) \(y = \cos 3x\);
c) \(y = {\log _2}\left( {{x^2} + 2} \right)\).
a, \(y=\left(2x^3+3\right)^2\)
\(y'=2\left(2x^3+3\right)6x^2\)
\(=12x^2\left(2x^3+3\right)\)
b,\(y=cos3x\)
\(y'=-3sin3x\)
c, \(y=log_2\left(x^2+2\right)\)
\(y'=\dfrac{2x}{\left(x^2+2\right)ln2}\)
Đúng 1
Bình luận (0)