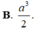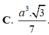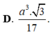Cho hình chóp SABC có AB=a, BC= a 3 , A B C ⏜ = 30 0 . Tam giác SAB đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối chóp SABC.
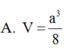
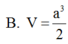

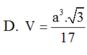
Cho hình chóp SABC có đáy là tam giác ABC vuông tại B, AB= 3a, BC= 4a (SBC) vuông ( ABC), SB= 2a căn 3, góc SBC= 30.
a. Tính V(SABC)
b. Tính d(B;(SAC))
Cho hình chóp SABC có A B = a , B C = a 3 , A B C ^ = 30 ° . Tam giác SAB đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Thể tích của khối chóp SABC bằng
A. a 3 8
B. a 3 2
C. a 3 3 7
D. a 3 3 17
cho hình chóp sabc có sa=sb=sc=2a, tam giác vuông tại a có ab=a/2, bc=a. tính thể tích khối chóp sabc
\(AC=\sqrt{BC^2-AB^2}=\dfrac{a\sqrt{3}}{4}\)
Gọi H là hình chiếu vuông góc của S lên đáy
Do \(SA=SB=SC\Rightarrow HA=HB=HC\Rightarrow H\) là tâm đường tròn ngoại tiếp ABC
Mà ABC vuông tại A \(\Rightarrow H\) là trung điểm BC
\(\Rightarrow BH=\dfrac{1}{2}BC=\dfrac{a}{2}\)
\(\Rightarrow SH=\sqrt{SB^2-BH^2}=\dfrac{a\sqrt{15}}{2}\)
\(V=\dfrac{1}{3}SH.\dfrac{1}{2}AB.AC=\dfrac{1}{3}.\dfrac{a\sqrt{15}}{2}.\dfrac{1}{2}.\dfrac{a}{2}.\dfrac{a\sqrt{3}}{4}=\dfrac{a^3\sqrt{5}}{32}\)
Cho hình chóp SABC có AB=a, A B = a 3 , A B C ^ = 30 ° . Tam giác SAB đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối chóp SABC.
A. V = a 3 8
B. V = a 3 2
C. V = a 3 3 7
D. V = a 3 3 17
Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại B, AB=BC=a\(\sqrt{3}\) , SAB=SCB=90\(^o\) và khoảng cách từ A đến (SBC) bằng a\(\sqrt{2}\) . Tính diện tích mặt cầu ngoại tiếp hình chóp SABC theo a
Lời giải:
Gọi $H$ là chân đường cao kẻ từ $S$ xuống mặt phẳng $(ABC)$
Ta có \(\left\{\begin{matrix} SH\perp AB\\ SA\perp AB\end{matrix}\right.\Rightarrow AB\perp (SHA)\rightarrow AB\perp HA\)
Tương tự \(BC\perp HC\). Kết hợp với \(ABC\) vuông cân tại $B$ suy ra \(ABCH\) là hình vuông
Có \(AH\parallel (SBC)\Rightarrow d(A,(SBC))=d(H,(SBC))\)
Kẻ \(HT\perp SC\). Có \(\left\{\begin{matrix} SH\perp BC\\ HC\perp BC\end{matrix}\right.\Rightarrow BC\perp (SHC)\Rightarrow BC\perp HT\)
Do đó \(HT\perp (SBC)\Rightarrow d(H,(SBC))=HT=\sqrt{\frac{SH^2.HC^2}{SH^2+HC^2}}=\sqrt{\frac{SH^2.AB^2}{SH^2+AB^2}}=\sqrt{2}\Rightarrow SH=\sqrt{6}a\)
Từ trung điểm $O$ của $AC$ dựng trục vuông góc với mặt phẳng $(ABC)$. Trên trục đó ta lấy điểm $I$ là tâm mặt cầu ngoại tiếp.
\(IS^2=IA^2=IH^2\Leftrightarrow (\overrightarrow{IO}+\overrightarrow{OH}+\overrightarrow{HS})^2=IO^2+OH^2\)
\(\Leftrightarrow HS^2+2\overrightarrow{IO}.\overrightarrow{HS}=0\)
Do \(\overrightarrow {SH}\parallel \overrightarrow {IO}\Rightarrow \overrightarrow {IO}=k\overrightarrow{SH}\). Thay vào PT trên có $k=\frac{1}{2}$
\(\Rightarrow IO=\frac{\sqrt{6}a}{2}\Rightarrow IA=\sqrt{IO^2+AO^2}=\sqrt{3}a\)
\(\Rightarrow S_{\text{mặt cầu}}=4\pi R^2=12a^2\pi\)
Cho hình chóp SABC có các cạnh bên bằng nhau và bằng 2a, Biết tam giác ABC cân tại A có AB= 2a, BC= 3a. Tính thể tích của khối chóp SABC
Gọi H là hình chiếu vuông góc của S lên đáy \(\Rightarrow\) H là tâm đường tròn ngoại tiếp tam giác ABC
Gọi M là trung điểm BC, do tam giác cân tại A \(\Rightarrow H\in AM\)
Kéo dài AM cắt đường tròn ngoại tiếp tam giác tại D \(\Rightarrow\widehat{ABD}\) là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow\Delta ABD\) vuông tại B
\(BM=\dfrac{1}{2}BC=\dfrac{3a}{2}\) \(\Rightarrow AM=\sqrt{AB^2-BM^2}=\dfrac{a\sqrt{7}}{2}\)
Áp dụng hệ thức lượng:
\(AB^2=AM.AD\Rightarrow AD=\dfrac{AB^2}{AM}=\dfrac{8a\sqrt{7}}{7}\)
\(\Rightarrow AH=\dfrac{AD}{2}=\dfrac{4a\sqrt{7}}{7}\)
\(\Rightarrow SH=\sqrt{SA^2-AH^2}=\dfrac{2a\sqrt{21}}{7}\)
\(V=\dfrac{1}{3}SH.\dfrac{1}{2}AM.BC=...\)
cho hình chóp đều SABC có SA=2a, AB=a. Gọi M là trung điểm BC. Tính theo a thế tích khối chóp SABC và khoảng cách giữa hai đường thẳng AM và SB.
Do SABC là hình chóp đều=>hình chiếu của S lên (ABC) là tâm I củađường tròn ngoại tiếp tam giác ABC=> SI vuông góc với (ABC)
xét tam giác SAI vuông tạị I , biết SA, AI=2/3 AM(là đường cao tgiacs ABC)=> tính được SI
V=1/3. SI.S(ABC)=(căn 11)/12
b) trong (ABC) kẻ hình bình hành AINB
d(AM,SB)=d(AI,SB)=d(I,SBN)( do AI song song AN)=> đưa về tính khoang cách trong tứ diện vuông cơ bản
Cho hình chóp SABC có các cạnh bên nghiêng đều trên đáy một góc 60 độ. Biết tam giác ABC có AB=a, AC=2a, BC=5a/2. Tính thể tích khối chóp SABC
Gọi H là hình chiếu vuông góc của S lên đáy
\(\Rightarrow\widehat{SAH}=\widehat{SBH}=\widehat{SCH}=60^0\)
\(\Rightarrow AH=BH=CH=\dfrac{SH}{tan60^0}\Rightarrow H\) là tâm đường tròn ngoại tiếp tam giác đáy
\(\Rightarrow AH=R=\dfrac{AB.BC.AC}{4S_{ABC}}\)
\(\Rightarrow SH=AH.tan60^0=\dfrac{AB.BC.AC.\sqrt{3}}{4S_{ABC}}\)
\(V=\dfrac{1}{3}SH.S_{ABC}=\dfrac{1}{3}.\dfrac{AB.BC.CA.\sqrt{3}}{4S_{ABC}}.S_{ABC}=\dfrac{5a^3\sqrt{3}}{12}\)
Cho hình chóp SABC có đáy là tam giác ABC vuông tại B. SA vuông góc với(ABC), AB = a, AC = 3a, SA = 2a.
a. chứng minh BC vuông góc (ABC).
b. Tính thể tích khối chóp SABC.
Cho hình chóp SABC có A B = α , B C = α 3 , A B C ^ = 30 ° Tam giác SAB đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Thể tích của khối chóp SABC bằng