Hàm số y = ( 1 - cos 2 x ) có chu kì là:
A. 2π
B. 2 π
C. π
D. π
Khẳng định nào sau đây là sai?
A. Hàm số \(y = \cos x\) có tập xác định là \(\mathbb{R}\)
B. Hàm số \(y = \cos x\) có tập giá trị là [-1;1]
C. Hàm số \(y = \cos x\) là hàm số lẻ
D. Hàm số \(y = \cos x\) tuần hoàn với chu kỳ \(2\pi \)
Ta có: \(y = \cos x\)
\(y\left( { - x} \right) = \cos \left( { - x} \right) = \cos x = y\)
Suy ra hàm số \(y = \cos x\) là hàm số chẵn
Vậy ta chọn đáp án C
1) Tìm giá trị lớn nhất của hàm số y = 2 Cos2x + Sin2x
2) Tìm giá trị lớn nhất của hàm số y = Sin2018x +
Cos2018x
3) Tìm chu kì T0 của hàm số f(x) = tan2x
4) Xác định chu kì của hàm số y = Sinx
5) Hàm số y = Sin2x là hàm số tuần hoàn, có chu kì là bao nhiêu
AI GIÚP EM VỚI Ạ, CHỨ EM VÃ LẮM RỒI HUHU. TRÌNH BÀY MỘT XÍU XIU CHO EM HIỂU NỮA THÌ CÀNG TỐT Ạ :(( EM CẢM ƠN NHIỀU LẮM Ạ.
Một chất điểm dao động điều hoà (dạng hàm cos) có chu kì T, biên độ A. Tốc độ trung bình của chất điểm khi pha của dao động biến thiên từ - 2 π / 3 đến π / 3 bằng
A. 3A/T
B. 4A/T
C. 3,6A/T
D. 2A/T
hàm số y=Cos(Sinx) có chu kì T là bao nhiêu?
Ta có \(y\left(x+\pi\right)=cos\left[sin\left(x+\pi\right)\right]=cos\left(-sinx\right)=cos\left(sinx\right)\)
nên \(y\left(x+2\pi\right)=y\left(x\right)\)
Tuần hoàn với chu kì π
TXĐ: \(D=R\)
Với mọi \(x\in R\) thì \(x+\pi\in R\)
Ta có:
\(f\left(x\right)=cos\left(sinx\right)\)
\(f\left(x+\pi\right)=cos\left(sin\left(x+\pi\right)\right)=cos\left(-sinx\right)=cos\left(sinx\right)=f\left(x\right)\)
\(\Rightarrow\) Hàm tuần hoàn với chu kì \(T=\pi\)
Giả sử tồn tại \(0< T_0< \pi\) sao cho \(f\left(x+T_0\right)=f\left(x\right)\); \(\forall x\)
\(\Leftrightarrow cos\left[sin\left(x+T_0\right)\right]=cos\left(sinx\right)\)
Thay \(x=0\Rightarrow cos\left(sinT_0\right)=cos0=1\) (1)
Do \(0< T_0< \pi\Rightarrow0< sinT_0< 1\Rightarrow cos\left(sinT_0\right)< 1\)
\(\Rightarrow\) (1) sai hay điều giả sử là sai
Vậy \(T=\pi\) là chu kì của hàm đã cho
Cho các mệnh đề sau
(I) Hàm số f x = sin x x 2 + 1 là hàm số chẵn.
(II) Hàm số f x = 3 sin x + 4 cos x có giá trị lớn nhất là 5.
(III) Hàm số f x = tan x tuần hoàn với chu kì 2 π .
(IV) Hàm số f x = cos x đồng biến trên khoảng 0 ; π .
Trong các mệnh đề trên có bao nhiêu mệnh đề đúng?
A. 4.
B. 2.
C. 3.
D. 1.
Cho hàm số y=f(x) có đồ thị hàm số y=f '(x) như hình vẽ bên. Số điểm cực trị của hàm số y=f(2sinx-1) trên khoảng - 2 π ; 2 π là
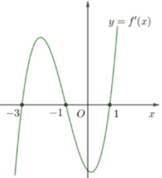
A.6
B. 8
C. 7
D. 5
Ta có
![]()
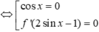
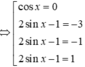
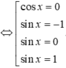
Đối chiếu với
x
∈
-
2
π
;
2
π
nhận 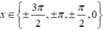 Qua tất cả các điểm này thì y′ đều đổi dấu, do đó hàm số có tất cả 7 điểm cực trị trên khoảng (−2π;2π).
Qua tất cả các điểm này thì y′ đều đổi dấu, do đó hàm số có tất cả 7 điểm cực trị trên khoảng (−2π;2π).
Chọn đáp án C.
Mẹo TN: Chọn ![]() thỏa mãn, khi đó
thỏa mãn, khi đó ![]() MODE 7 trên khoảng (−2π;2π) có 7 lần đổi dấu tức có 7 điểm cực trị trên khoảng (−2π;2π).
MODE 7 trên khoảng (−2π;2π) có 7 lần đổi dấu tức có 7 điểm cực trị trên khoảng (−2π;2π).
Chọn đáp án C.
tìm chu kì của hàm số
f(x)= cos^2 x
f(x)=|cos x|
Xét tính tuần hoàn và tìm chu kì (nếu có) của hàm số sau: y = cosx + cos( 3 x)
A: hàm số không tuần hoàn
B: Hàm số tuần hoàn với T = 2π
C: Hàm số tuần hoàn với T = π
D: Tất cả sai
Số nghiệm của phương trình cos x =1/2 thuộc - 2 π ; 2 π là
A. 4
B. 2
C. 3
D. 1
Khẳng định nào sau đây là sai?
A. Hàm số y=cosx
có tập xác định là R
B. Hàm số y=cosx
có tập giá trị là [-1;1]
C. Hàm số y=cosx
là hàm số lẻ
D. Hàm số y=cosx tuần hoàn với chu kỳ 2π