Xét n là số nguyên dương và 1 + x n = a 0 + a 1 x + a 2 x 2 + . . . + a k x k + . . . + a n x n . Biết rằng tồn tại số nguyên k , 1 ≤ k ≤ n - 1 , sao cho a k - 1 2 = a k 9 = a k + 1 24 . Giá trị của a 2 bằng
A. 66
B. 36
C. 55
D. 45
PB
Những câu hỏi liên quan
Xét biểu thức lôgic:(n>0) and (n mod 2 = 0). Khẳng định nào sau đây là đúng?
A. Kiểm tra xem n có là số nguyên dương chẵn không
B. Kiểm tra xem n có là một số dương không
C. Kiểm tra n có chia hết cho 2 không
D. Kiểm tra n là một số nguyên chẵn không
Xét biểu thức lôgic:(n>0) and (n mod 2 = 0). Khẳng định nào sau đây là đúng?
A. Kiểm tra xem n có là số nguyên dương chẵn không
B. Kiểm tra xem n có là một số dương không
C. Kiểm tra n có chia hết cho 2 không
D. Kiểm tra n là một số nguyên chẵn không
b1:Xét cặp số nguyên dương (a,b) thỏa mãn điều kiện abba=72.Hỏi a+b nhận giá trị lớn nhất là bao nhiêu
b2:Hỏi có bao nhiêu cặp số nguyên dương (x,y)sao cho 1/x+1/y=1/2020
b3:tìm số nguyên dương N nhỏ nhất ,chia hết cho 99 và tất cả các chữ số của N đều chẵn
Mình không biết nha tạm thời bạn hỏi bạn khác đi 😅
xét số n là tích của 10 số nguyên dương lớn hơn 1 và đôi một phân biệt hỏi n có ít nhất bao nhiêu ước nguyên dương
Giả sử n là tích của 10 số sau :
a1 x a2 x a3 x a4 x a5 x a6 x a7 x a8 x a9 x a10
Nếu 10 số trên đều có UCLN = 1 thì N có ít ước nguyên dương nhất
Như vậy n sẽ được phân tích dưới dạng thừa số nguyên tố là :
a11 x a21 x a31 x a41 x a51 x a61 x a71 x a81 x a91 x a101
Số ước của n sẽ là ( 1 + 1)(1+1)....(1+1) = 2 x 2 x...x 2 ( 10 lần số 2) = 210 = 1024
Xét n là số nguyên dương thỏa mãn điều kiện
C
n
+
4
n
+
1
-
C
n
+
3
n
7
n
+
3
. Hệ số của số hạng chứa
x
8
...
Đọc tiếp
Xét n là số nguyên dương thỏa mãn điều kiện C n + 4 n + 1 - C n + 3 n = 7 n + 3 . Hệ số của số hạng chứa x 8 trong khai triển 1 x 3 + x 5 n với x > 0, bằng
A. 549
B. 954
C. 945
D. 495
Xét n là số nguyên dương thỏa mãn điều kiện
C
n
1
+
3
C
n
2
145
. Số hạng không chứa x trong khai triển của biểu thức
x
4
-
3
x
n
,
x
≠
0...
Đọc tiếp
Xét n là số nguyên dương thỏa mãn điều kiện C n 1 + 3 C n 2 = 145 . Số hạng không chứa x trong khai triển của biểu thức x 4 - 3 x n , x ≠ 0 bằng
A. 295245
B. 59049
C. – 59049
D. – 295245
Xét những số được tạo thành bằng cách viết 2n chữ số 0 và 2n+1 chữ số 1 xen kẽ nhau, ví dụ 10101, 1010101,.......( n là số nguyên dương) Chứng minh các số tạo thành đều là hợp số.
Cho x≠0 và x +1/x là một số nguyên. Khi đó với mọi số nguyên dương n, có kết luận gì về T ( n , x ) = x n + 1 x n
A. T(n,x) là số vô tỉ
B. T(n,x) là số không nguyên
C. T(n,x) là số nguyên
D. Các kết luận trên đều sai
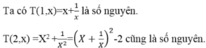
\Ta sẽ chứng minh T(1,x) là số nguyên
Thật vậy, áp dụng phép chứng minh quy nạp, Ta có:
Bước cơ sở: T(1,x) là số nguyên. Khẳng định đúng với n=1
Bước quy nạp: Giả sử T(n,x) là số nguyên với mọi n≥1. Ta sẽ chứng minh T(n+1,x) cũng là số nguyên
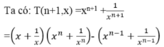
=T(1,x).T(n,x) – T(n-1,x).
Theo giả thuyết quy nạp, Ta có T(1,x),T(n,x), T(n-1,x) là các số nguyên nên T(n+1,x) là số nguyên
Chọn C
Đúng 0
Bình luận (0)
Hãy xem trong lời giải của bài toán sau đây có bước nào bị sai?Bài toán: chứng minh rằng với mọi số nguyên dương n, mệnh đề sau đây đúng:A(n) : “nếu a và b là những số nguyên dương mà max{a,b} n thì a b”Chứng minh :Bước 1: A(1):”nếu a,b là những số nguyên dương mà max{a,b} 1 thì a b”Mệnh đề A(1) đúng vì max{a,b} 1 và a,b là những số nguyên dương thì a b 1.Bước 2: giả sử A(k) là mệnh đề đúng vơi k≥1Bước 3: xét max{a,b} k+1 ⇒max{a-1,b-1} k+ 1-1 kDo a(k) là mệnh đề đúng nên a- 1 b-1 ⇒ a b⇒...
Đọc tiếp
Hãy xem trong lời giải của bài toán sau đây có bước nào bị sai?
Bài toán: chứng minh rằng với mọi số nguyên dương n, mệnh đề sau đây đúng:
A(n) : “nếu a và b là những số nguyên dương mà max{a,b} = n thì a = b”
Chứng minh :
Bước 1: A(1):”nếu a,b là những số nguyên dương mà max{a,b} = 1 thì a = b”
Mệnh đề A(1) đúng vì max{a,b} = 1 và a,b là những số nguyên dương thì a= b =1.
Bước 2: giả sử A(k) là mệnh đề đúng vơi k≥1
Bước 3: xét max{a,b} = k+1 ⇒max{a-1,b-1} = k+ 1-1 = k
Do a(k) là mệnh đề đúng nên a- 1= b-1 ⇒ a= b⇒ A(k+1) đúng.
Vậy A(n) đúng với mọi n ∈N*
A. Bước 1
B. Bước 2
C. Bước 3
D. Không có bước nào sai
Đáp án là C. Ta có a,b∈N* không suy ra a -1, b -1∈N* . Do vậy không áp dụng được giả thiết quy nạp cho cặp {a -1, b -1}.
Chú ý: nêu bài toán trên đúng thì ta suy ra mọi số tự nhiên đều bằng nhau. Điều này là vô lí.
Đúng 0
Bình luận (0)
viết chương trình nhập vào 1 số nguyên dương N. Xét xem N có là tổng của nhiều số nguyên dương liên tiếp ko.
python
n = int(input("Nhập số nguyên dương N: "))
found = False
for i in range(1, n//2+1):
sum = i
j = i + 1
while sum < n:
sum += j
j += 1
if sum == n:
found = True
start = i
end = j - 1
break
if found:
print(n, "có tổng của nhiều số nguyên dương liên tiếp:")
for k in range(start, end+1):
print(k, end=" ")
else:
print(n, "không có tổng của nhiều số nguyên dương liên tiếp.")
Đúng 0
Bình luận (0)