Cho hình lăng trụ đứng ABC. A 1 B 1 C 1 có tất cả các cạnh đều bằng nhau và bằng a. Các đáy của lăng trụ nội tiếp các đường tròn đáy của khối trụ (H). Thể tích của khối trụ là:
A. πa 3 3 3
B. πa 3 3
C. πa 3 9
D. 3 πa 3 4
Cho hình lăng trụ tam giác đều ABC.A'B'C' có tất cả các cạnh bằng nhau và bằng 2a . Tính cosin góc giữa (A'BC) và (ABC) .
Bài 1: Cho lăng trụ đứng có đáy là tam giác đều biết rằng tất cả các cạnh của lăng trụ bằng a. Tính thể tích và tổng diện tích các mặt bên của lăng trụ.
Thể tích của hình lăng trụ đã cho: V = \(\dfrac{a^2\sqrt{3}}{4}\).a = \(\dfrac{a^3\sqrt{3}}{4}\).
Tổng diện tích các mặt bên (diện tích xung quanh) của lăng trụ: Sxq = 3a.a = 3a2.
Cho lăng trụ đứng tam giác ABC.A'B'C' có tất cả các cạnh đều bằng a. Biết B A C ^ = 120 ° , tính thể tích V của hình lăng trụ
A. V = a 3 3 2
B. V = a 3 3 4
C. V = a 3 3
D. V = a 3
Cho hình lăng trụ \(ABCD.A'B'C'D'\). Biết \(A'.ABCD\) là hình chóp đều có tất cả các cạnh đều bằng nhau và bằng \(a\). Tính theo \(a\) thể tích của khối lăng trụ \(ABCD.A'B'C'D'\) và thể tích của khối chóp \(A'.BB'C'C\).
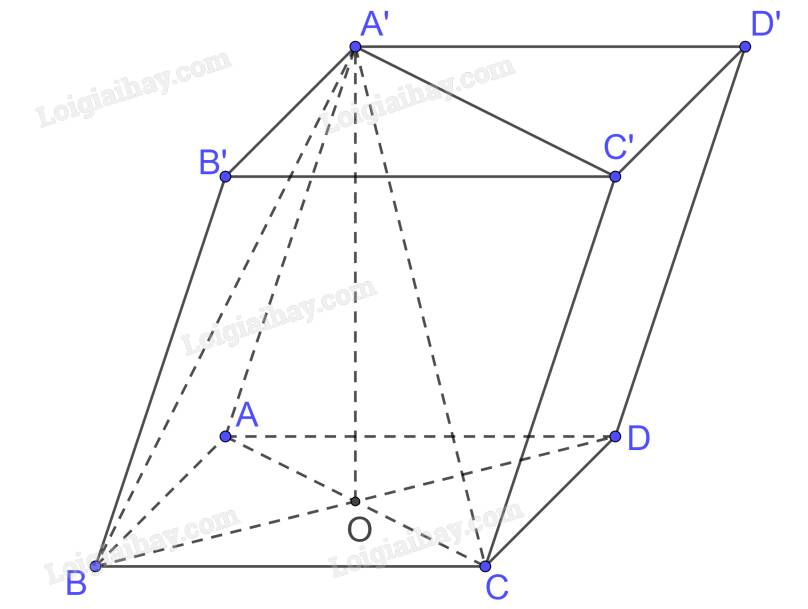
Gọi \(AC \cap BD = \left\{ O \right\}\) mà A’.ABCD là hình chóp đều nên \(A'O \bot \left( {ABCD} \right)\)
Xét tam giác ABC vuông tại B có \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
\( \Rightarrow OA = \frac{{AC}}{2} = \frac{{a\sqrt 2 }}{2}\)
Xét tam giác A’AO vuông tại O có
\(A'O = \sqrt {A{{A'}^2} - A{O^2}} = \sqrt {{a^2} - {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}} = \frac{{a\sqrt 2 }}{2}\)
\({S_{ABCD}} = {a^2}\)
Vậy khối lăng trụ có thể tích \(V = \frac{1}{3}A'O.{S_{ABCD}} = \frac{1}{3}.\frac{{a\sqrt 2 }}{2}.{a^2} = \frac{{{a^3}\sqrt 2 }}{6}\)
Nếu hình lăng trụ \(ABCD.A'B'C'D'\) xoay lại thành hình lăng trụ AA’D’D.BB’C’C thì thể tích không thay đổi do đó thể tích hình chóp \(A'.BB'C'C\) bằng một phần 3 thể tích hình lăng trụ AA’D’D.BB’C’C vì chung đáy và chung chiều cao kẻ từ A’ xuống đáy BB’C’C.
Thể tích khối chóp là \({V_{A'.BB'C'C}} = \frac{1}{3}.\frac{{{a^3}\sqrt 2 }}{6} = \frac{{{a^3}\sqrt 2 }}{{18}}\)
Cho hình lăng trụ tam giác đều ABC.A¢B¢C¢ có tất cả các cạnh đều bằng a. Tính diện tích của mặt cầu ngoại tiếp hình lăng trụ theo a.
A. S = 17 πa 2 13
B. S = 7 πa 2 3
C. S = 17 πa 2
D. S = 7 π a 2
Cho lăng trụ ABC.A′B′C′ có tất cả các cạnh bằng 1, hình chiếu vuông góc của A′ lên mặt phẳng (ABC) trùng với trung điểm cạnh AB. Côsin góc giữa hai mặt phẳng (A′BC) và (AB′C′) bằng
A. 65 65
B. 2 26 13
C. 143 13
D. 65 13
Gọi O là trung điểm cạnh
A
B
⇒
A
'
O
⊥
(
A
B
C
)
và 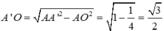 Lập hệ trục toạ độ Oxyz với các tia Ox, Oy, Oz lần lượt trùng với các tia OC, OB, OA’. Toạ độ các đỉnh là o(0;0;0),
Lập hệ trục toạ độ Oxyz với các tia Ox, Oy, Oz lần lượt trùng với các tia OC, OB, OA’. Toạ độ các đỉnh là o(0;0;0),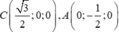

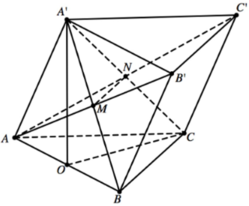
Suy ra ![]()
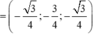
Và
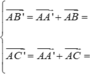
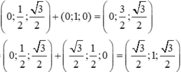
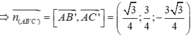
Vậy ![]()
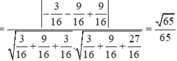
Chọn đáp án A.
Cách 2: Có thể dùng công thức thể tích tứ diện cho TH đặc biệt:
![]()
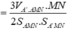
Chọn đáp án A.
Cho (H) là khối lăng trụ đứng tam giác đều có tất cả các cạnh bằng a.
A. a 3 2 B. a 3 3 2
C. a 3 3 4 D. a 3 2 3
Chọn C.
Để ý rằng diện tích tam giác đều cạnh a bằng a 3 3 4
Cho hình lăng trụ đứng tam giác ABC.A’B’C’ có tất cả các cạnh đều bằng a. Tính thể tích khối tứ diện A’BB’C’.
Ta chia khối lẳng trụ đã cho thành hình chóp A’.ABC, C.A’B’C’ và C.A’BB’
Ta có: VA’.ABC = VA’B’C’ = 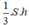 trong đó S là diện tích đáy S = SABC = SA’B’C’ và h là chiều cao của hình lăng trụ
trong đó S là diện tích đáy S = SABC = SA’B’C’ và h là chiều cao của hình lăng trụ
Lại có: VABC.A’B’C’ = S.h
Do đó,
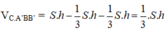
Trong đó, tam giác ABC là tam giác đều có độ dài cạnh bằng a nên 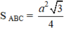
Vì đây là hình lăng trụ đứng nên h = AA’ = BB’= CC’ = a.
Vậy thể tích hình chóp C.A’BB’ là:
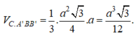
Cho hình lăng trụ đứng tam giác ABC.A’B’C’ có tất cả các cạnh đều bằng a. Mặt phẳng đi qua A’B’ và trọng tâm tam giác ABC, cắt AC và BC lần lượt tại E và F. Tính thể tích hình chóp C.A’B’FE.
Gọi I, K lần lượt là trung điểm của AB và A’B’, G là trọng tâm của tam giác ABC.Đường thẳng qua G, song song với AB cắt AC và BC lần lượt tại E và F, đường thẳng EF chính là giao tuyến của hai mặt phẳng (GA’B’) và (ABC).

