Cho x là số thực dương thỏa mãn: 3 2 x + 9 = 10 . 3 x Tính giá trị của x 2 + 1
A. 1.
B. 5.
C. 1 và 5.
D. 0 và 2.
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Cho x là số thực dương thỏa mãn 3 2 x + 3 = 4 .3 x . Tính giá trị của x 2 − 1 .
A. 0
B. 0 và -1
C. 0 và 1
D. 1
Cho x là số thực dương thỏa mãn 3 2 x + 3 = 4 . 3 x . Tính giá trị của x 2 - 1
A. 0 và 1
B. 0
C. 0 và -1
D. 1
Cho x,y là các số thực dương thỏa mãn x+y+xy=3 tìm các giá trị lớn nhất của biểu thức
\(P=\sqrt{9-x^2}+\sqrt{9-y^2}+\dfrac{x+y}{4}\)
\(3=x+y+xy\le\sqrt{2\left(x^2+y^2\right)}+\dfrac{x^2+y^2}{2}\)
\(\Rightarrow\left(\sqrt{x^2+y^2}-\sqrt{2}\right)\left(\sqrt{x^2+y^2}+3\sqrt{2}\right)\ge0\)
\(\Rightarrow x^2+y^2\ge2\)
\(\Rightarrow-\left(x^2+y^2\right)\le-2\)
\(P=\sqrt{9-x^2}+\sqrt{9-y^2}+\dfrac{x+y}{4}\le\sqrt{2\left(9-x^2+9-y^2\right)}+\dfrac{\sqrt{2\left(x^2+y^2\right)}}{4}\)
\(P\le\sqrt{2\left(18-x^2-y^2\right)}+\dfrac{1}{4}.\sqrt{2\left(x^2+y^2\right)}\)
\(P\le\left(\sqrt{2}-1\right)\sqrt{18-x^2-y^2}+\sqrt[]{2}\sqrt{\dfrac{\left(18-x^2-y^2\right)}{2}}+\dfrac{1}{2}\sqrt{\dfrac{x^2+y^2}{2}}\)
\(P\le\left(\sqrt{2}-1\right).\sqrt{18-2}+\sqrt{\left(2+\dfrac{1}{4}\right)\left(\dfrac{18-x^2-y^2+x^2+y^2}{2}\right)}=\dfrac{1+8\sqrt{2}}{2}\)
Dấu "=" xảy ra khi \(x=y=1\)
Cho x, y là các số thực dương thỏa mãn: \(x^3+y^3-6.\left(x^2+y^2\right)+13.\left(x+y\right)-20=0\). Tính giá trị của: \(A=x^3+y^3+12xy\)
Đặt \(x+y=a\Leftrightarrow a-4=x+y-4\)
\(x^3+y^3-6\left(x^2+y^2\right)+13\left(x+y\right)-20=0\\ \Leftrightarrow\left(x+y\right)^3-6\left(x+y\right)^2+13\left(x+y\right)-20-3xy\left(x+y\right)+12xy=0\\ \Leftrightarrow a^3-6a^2+13a-20-3xy\left(x+y-4\right)=0\\ \Leftrightarrow a^3-4a^2-2a^2+8a+5a-20-3xy\left(a-4\right)=0\\ \Leftrightarrow\left(a-4\right)\left(a^2-2a+5\right)-3xy\left(a-4\right)=0\\ \Leftrightarrow\left(a-4\right)\left(a^2-2a+5-3xy\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}a=4\\a^2-2a+5-3xy=0\left(vô.n_0\right)\end{matrix}\right.\\ \Leftrightarrow x+y=4\)
\(\Leftrightarrow A=x^3+y^3+12xy=\left(x+y\right)^3-3xy\left(x+y\right)+12xy\\ A=4^3-3xy\left(x+y-4\right)=64-0=64\)
cho x,y là số thực dương thỏa mãn x^3+y^3=xy-1/27
tính giá trị của biểu thức P=(x+y+1/3)^3-3/2(x+y)+2018
chịu but Merry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry ChristmasMerry Christmas
Cho $x$, $y$ là các số thực dương thỏa mãn $x + y \le 3$. Tìm giá trị nhỏ nhất của biểu thức $Q = x^2 + y^2 - 9 x - 12 y + \dfrac{16}{2x+y} + 25.$
Cho x, y là các số thực dương thỏa mãn điều kiện 5 x + 2 y + 3 3 x y + x + 1 = 5 x y 5 + 3 − x − 2 y + y x − 2 . Tính giá trị nhỏ nhất của biểu thức T=x+y
A. T min = 2 + 3 2
B. T min = 3 + 2 3
C. T min = 3 2
D. T min = 5 + 3 2
Cho x, y là các số thực dương thỏa mãn điều kiện 5 x + 2 y + 3 3 x y + x + 1 = 5 x y 5 + 3 - x - 2 y + y x - 2 . Tính giá trị nhỏ nhất của biểu thức T = x + y
A. T m i n = 2 + 3 2
B. T m i n = 3 + 2 3
C. T m i n = 1 + 5
D. T m i n = 5 + 3 2
Đáp án B.
Từ giả thiết, suy ra 5 x + 2 y + 1 3 x y - 1 + x + 1 = 5 x y - 1 + 1 3 x + 2 y + x y - 2 y
⇔ 5 x + 2 y - 1 3 x + 2 y + x + 2 y = 5 x y - 1 - 1 3 x y - 1 + ( x y - 1 ) (1)
Xét hàm số f ( t ) = 5 t - 1 3 t + t trên ℝ .
Đạo hàm f ' ( t ) = 5 t . ln 5 + ln 3 3 t + 1 > 0 , ∀ t ∈ ℝ ⇒ hàm số f (t) luôn đồng biến trên ℝ .
Suy ra 1 ⇔ f ( x + 2 y ) = f ( x y - 1 ) ⇔ x + 2 y = x y - 1 ⇔ x + 1 = y ( x - 2 )
y = x + 1 x - 2
Do y > 0 nên x + 1 x - 2 > 0 ⇔ x > 2 x < - 1 . Mà x > 0 nên x > 2.
Từ đó T = x + y = x + x + 1 x - 2 . Xét hàm số g ( x ) = x + x + 1 x - 2 trên 2 ; + ∞ .
Đạo hàm g ' ( x ) = 1 - 3 x - 2 2 > 0 , g ' ( x ) = 0 ⇔ ( x - 2 ) 2 = 3
⇔ x = 2 + 3 ( t m ) x = 2 - 3 ( L ) . Lập bảng biến thiên của hàm số trên 2 ; + ∞ , ta thấy m i n g ( x ) = g ( 2 + 3 ) = 3 + 2 3 .
Vậy T m i n = 3 + 2 3 khi x = 2 + 3 và y = 1 + 3 .
Cho x,y là các số thực dương thỏa mãn điều kiện 5 x + 2 y + 3 3 x y + x + 1 = 5 x y 5 + 3 - x - 2 y + y x - 2
Tính giá trị nhỏ nhất của biểu thức T =x + y.
A. T m i n = 2 + 3 2
B. T m i n = 3 + 2 3
C. T m i n = 1 + 5
D. T m i n = 5 + 3 2
Từ giả thiết ta suy ra
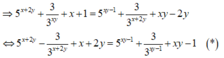
Xét hàm số f ( t ) = 5 t - 1 3 t + t với t ∈ ℝ , f ' ( t ) = 5 t . ln 5 + 3 - t . ln 3 + 1 > 0 ; ∀ t ∈ ℝ
Suy ra y= f( t) là hàm số đồng biến trên R mà từ ( * ) suy ra
f (x+ 2y) =f( xy-1) hay x+ 2y= xy-1
![]()
với x>0 suy ra y>1.
Khi đó
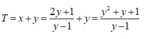
Xét hàm số
f ( y ) = y 2 + y + 1 y - 1 t r ê n 1 ; + ∞ f ' y = y 2 - 2 y - 2 y - 1 2 = 0 ⇔ y = ± 1 + 3 f 1 + 3 = 3 + 2 3 ; lim y → 1 f ( y ) = lim y → + ∞ f ( y ) = + ∞
Do đó, giá trị nhỏ nhất của hàm số là 3 + 2 3 .
Vậy kết quả là 3 + 2 3
Chọn B.