x = 0; 4π; k = 6

x = 5π/4; k = 1

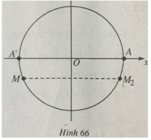
(h.66) Ta có

A M 2  = MA’ = MA + AA’

Suy ra

Sđ A M 2  = -α + π + k2π, k ∈ Z.

Vậy đáp án là B.

6.13. (h.67) Ta có

Sđ A M 3  = -sđ AM = -α + k2π, k ∈ Z.

Đáp án: D

a) \(a=12,4\pi=12\pi+0,4\pi=6.2\pi+0,4\pi\).
Suy ra: \(x=0,4\pi\).
b) \(a=-\dfrac{9}{5}\pi=-2\pi+\dfrac{1}{5}\pi\).
Suy ra: \(x=\dfrac{1}{5}\pi\).
c) \(a=\dfrac{13}{4}\pi=2\pi+\dfrac{5}{4}\pi\)
Suy ra: \(x=\dfrac{5}{4}\pi\).

31+(x-20)=121

31+(x-20)=121 bằng bao nhiêu v

1:

A={1;-1;2;-2}

B={0;1;2;3;4}

B\A={0;3;4}

X là tập con của B\A

=>X={0;3;4}

P(x) = ax⁵ + by⁴ + cz³ + dt² + e (với x;y;z;g;e là 7 số tự nhiên liên tiếp và a;b;c;d là các hệ số nguyên)

Từ điều kiện c) ta có :

- Nếu số k đó là y hoặc t thì y = t = 0. Loại trường hợp này vì e là số tự nhiên mà e < t = 0

- Nếu số k đó là x; z hoặc e :

- Với k là x ta có ax⁵ + by⁴ + cz³ + dt² + e = 0   =>  -ax⁵ =  by⁴ + cz³ + dt² + e

Dễ thấy by⁴ + cz³ + dt² + e > 0  =>  -ax⁵ > 0 => .... tìm đc x

Tương tự tìm đc z hoăc e. Thử trong 3 số trên trường hợp nào thỏa mãn điều kiện b là ra.

Nhờ Kiệt giúp kìa

Ta có: (a+x) + (a-x) = 11 + 27 

 2a + x - x = 38

2a = 38

a=38:2

a=19

a) x= 11-a

b) x= a- 27

Ta có : x = 11 - a 

           x = a - 27

Khi đó : 11- a = a - 27

            11 + 27 = a + a 

            38 = 2a 

            a = 38 : 2

            a = 19

x = 19 - 11 = (-8)