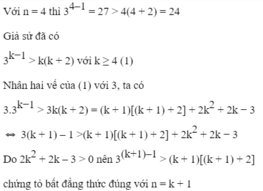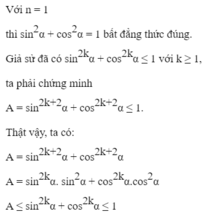Chứng minh các bất đẳng thức n n 2 + 1 ≤ 1 2 và n 2 + 1 2 n ≥ 1 với mọi n ∈ N * .
PB
Những câu hỏi liên quan
Chứng minh các bất đẳng thức sau ( n ∈ N ∗ ) 2 n + 2 > 2 n + 5
Với n = 1 thì 2 1 + 2 = 8 > 7 = 2 . 1 + 5
Giả sử bất đẳng thức đúng với n = k ≥ 1 tức là 2k + 2 > 2k + 5 (1)
Ta phải chứng minh nó cũng đúng với n = k + 1,
tức là 2k + 3 > 2(k + 1) + 5 hay 2k + 3 > 2k + 7(2)
Thật vậy, nhân hai vế của (1) với 2, ta được
2k + 3 > 4k + 10 = 2k + 7 + 2k + 3
Vì 2k + 3 > 0 nên 2k + 3 > 2k + 7(đpcm)
Đúng 0
Bình luận (0)
Chứng minh các bất đẳng thức sau 3n − 1 > n(n + 2) với n ≥ 4
Chứng minh các bất đẳng thức sau ( n ∈ N ∗ ) sin 2 n α + cos 2 n α ≤ 1 .
Chứng minh rằng với mọi số tự nhiên n ≥ 2 , ta có các bất đẳng thức: 2 n + 1 > 2 n + 3
2n + 1 > 2n + 3 (2)
+ Với n = 2 thì (2) ⇔ 8 > 7 (luôn đúng).
+ Giả sử (2) đúng khi n = k ≥ 2, nghĩa là 2k+1 > 2k + 3.
Ta chứng minh đúng với n= k+ 1 tức là chứng minh: 2k+2 > 2(k+ 1)+ 3
Thật vậy, ta có:
2k + 2 = 2.2k + 1
> 2.(2k + 3) = 4k + 6 = 2k + 2 + 2k + 4.
> 2k + 2 + 3 = 2.(k + 1) + 3 ( Vì 2k + 4 >3 với mọi k ≥ 2)
⇒ (2) đúng với n = k + 1.
Vậy 2n + 1 > 2n + 3 với mọi n ≥ 2.
Đúng 0
Bình luận (0)
Chứng minh bất đẳng thức Cô-si với n số không âm.
1) chứng minh bất đẳng thức Bu-nhi-a-cốp-ski với bộ n số.
Ai nhanh mình tick!^_^
Chứng minh bất đẳng thức sau biết a;b;m;n là các số nguyên: a ^ (m + n) + b ^ (m + n) >= a ^ m * b ^ n + a ^ n * b ^ m
chứng minh bất đẳng thức: m^2 + n^2 + p^2 + q^2 + 1 >= m(n + p + q + 1)
Áp dụng bất đẳng thức Cauchy ta có:
\(m^2+n^2+p^2+q^2+1\)
\(=\left(\frac{1}{4}m^2+n^2\right)+\left(\frac{1}{4}m^2+p^2\right)+\left(\frac{1}{4}m^2+q^2\right)+\left(\frac{1}{4}m^2+1\right)\)
\(\ge2\sqrt{\frac{1}{4}m^2\cdot n^2}+2\sqrt{\frac{1}{4}m^2\cdot p^2}+2\sqrt{\frac{1}{4}m^2\cdot q^2}+2\sqrt{\frac{1}{4}m^2\cdot1}\)
\(=2\cdot\frac{1}{2}mn+2\cdot\frac{1}{2}mp+2\cdot\frac{1}{2}mq+2\cdot\frac{1}{2}m\)
\(=mn+mp+mq+m\)
\(=m\left(n+p+q+1\right)\)
Dấu "=" xảy ra khi: \(\frac{1}{4}m^2=n^2=p^2=q^2=1\)\(\Rightarrow\hept{\begin{cases}m=2\\n=p=q=1\end{cases}}\)
Chứng minh các bất đẳng thức:
\(\left(a_1+a_2+...+a_n\right)^2\le n\left(a_1^2+a_2^2+...+a_n^2\right)\)
Sửa đề: n \(\ge1\).
Với n =1, bất đẳng thức trở thành đẳng thức.
Với n =2, cần chứng minh: \(2\left(a_1^2+a_2^2\right)\ge\left(a_1+a_2\right)^2\Leftrightarrow\left(a_1-a_2\right)^2\ge0\) (đúng)
Giả sử nó đúng đến n = k, tức là ta có: \(k\left(a_1^2+a_2^2+...+a_k^2\right)\ge\left(a_1+a_2+...+a_k\right)^2\)
Hay là: \(\left(a_1^2+a_2^2+...+a_k^2\right)\ge\frac{\left(a_1+a_2+...+a_k\right)^2}{k}\)
Ta c/m nó đúng với n = k +1 or \(\left(k+1\right)\left(a_1^2+a_2^2+...+a_k^2+a_{k+1}^2\right)\ge\left(a_1+a_2+...+a_k+a_{k+1}\right)^2\)
Ta có: \(VT=\left(k+1\right)\left(a_1^2+a_2^2+...+a_k^2+a_{k+1}^2\right)\)
\(\ge\left(k+1\right)\left[\frac{\left(a_1+a_2+...+a_k\right)^2}{k}+\frac{a^2_{k+1}}{1}\right]\ge\frac{\left(k+1\right)\left(a_1+a_2+..+a_k+a_{k+1}\right)^2}{k+1}=VP\)
Vậy đpcm là đúng.
P/s: Chả biết đúng không, chưa check, đại khái hướng làm là dùng quy nạp.
delllllllllll bt
ta có: 2(a^2+b^2)>= (a+b)^2
Xem thêm câu trả lời
Chứng minh rằng với mọi số tự nhiên n ≥ 2 , ta có bất đẳng thức: 3 n > 3 n + 1
Chứng minh: 3n > 3n + 1 (1)
+ Với n = 2 thì (1) ⇔ 9 > 7 (luôn đúng).
+ Giả sử (1) đúng với n = k ≥ 2, tức là 3k > 3k + 1.
Ta chứng minh đúng với n= k+1 tức là chứng minh: 3k+ 1 > 3(k+1) + 1
Thật vậy, ta có:
3k + 1 = 3.3k > 3.(3k + 1) (Vì 3k > 3k + 1 theo giả sử)
= 9k + 3
= 3k + 3 + 6k
= 3.(k + 1) + 6k
> 3(k + 1) + 1.( vì k ≥ 2 nên 6k ≥ 12> 1)
⇒ (1) đúng với n = k + 1.
Vậy 3n > 3n + 1 đúng với mọi n ≥ 2.
Đúng 0
Bình luận (0)