Cho tam giác ABC đều cạnh a ; H là trung điểm của BC. Tính C A → − H C → .
A. C A → − H C → = a 2 .
B. C A → − H C → = 3 a 2 .
C. C A → − H C → = 2 3 a 3 .
D. C A → − H C → = a 7 2 .
a)Cho tam giác ABC có các trung tuyến \(m_a=15;m_b=12;m_c=9\). Tính diện tích tam giác ABC.
b) Cho tam giác ABC đều cạnh a. Bán kính đường trọn ngoại tiếp tam giác ABC bằng?
c) Cho tam giác ABC đều cạnh 2a. Bán kính đường trọn ngoại tiếp tam giác ABC bằng?
Cho tam giác ABC là tam giác đều cạnh a. Bán kính đường tròn ngoại tiếp tam giác ABC bằng.
A. a 3 3
B. a 3 2
C. a 3 4
D. a 2 2
Áp dụng định lí sin trong tam giác ta có a sin A = 2 R . Suy ra:
R = a 2 sin 60 ° = a 2. 3 2 = a 3 3 .
Chọn A.
cho tam giác đều ABC có cạnh là a . tính diện tích tam giác ABC theo a
ABC đều nên đường cao của nó là trung tuyến cạnh đối diện nên đường cao là a:2 đáy là a diên tích tính theo công thức
từ A kẻ AH vuông góc với BC TA CÓ \(AH=\frac{a\sqrt{3}}{2}\)
\(\Rightarrow Sabc=\frac{1}{2}AH.BC=\frac{1.a\sqrt{3}}{2.2}a=a^2\frac{\sqrt{3}}{4}\)
Cho tam giác ABC đều có cạnh BC = a. Tính diện tích của tam giác ABC theo a.
chào các bạn
chào j mà chào
Áp dụng định lý Heron để suy ra, ta có công thức tính diện tích tam giác đều:
\(S\)ABC\(=a^2.\frac{\sqrt{3}}{4}\)
Hok tốt
Cho hình chóp SABC có đáy ABC là tam giác đều cạnh a Hình chiếu vuông góc của S lên (ABC )trùng với trung điểm H của cạnh BC biết tam giác SBC là tam giác đều tính số đo của góc giữa SA và (ABC)
\(SH\perp\left(ABC\right)\Rightarrow\widehat{SAH}\) là góc giữa SA và (ABC)
\(SH=\dfrac{a\sqrt{3}}{2}\) (đường trung tuyến trong tam giác đều SBC cạnh a)
\(AH=\dfrac{a\sqrt{3}}{2}\) (đường trung tuyến trong tam giác đều ABC cạnh a)
\(tan\widehat{SAH}=\dfrac{SH}{AH}=1\Rightarrow\widehat{SAH}=45^0\)
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm H của cạnh BC. Biết tam giác SBC là tam giác đều. Tính số đo của góc giữa SA và (ABC)
A. 300
B. 450
C. 600
D. 900
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S lên ( A B C ) trùng với trung điểm H của cạnh BC. Biết tam giác SBC là tam giác đều. Tính số đo của góc giữa SA và ( A B C ) .
A. 30 0
B. 45 0
C. 60 0
D. 90 0
Đáp án B
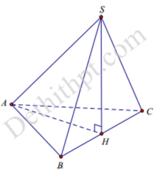
Vì hai tam giác ABC và SBC đều và có chung cạnh BC nên bằng nhau ⇒ A H = S H .
Mà Δ H S A vuông tại H nên vuông cân
⇒ S A H ^ = 45 °
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm H của cạnh BC. Biết tam giác SBC là tam giác đều. Tính số đo của góc giữa SA và (ABC).
A. 30 °
B. 75 °
C. 60 °
D. 45 °
Cho tam giác ABC vuông tại A và có BC = 2AB, AB = a. Ở phía ngoài tam giác, ta vẽ hình vuông BCDE, tam giác đều ABF và tam giác đều AGC. Tính các góc B, C, cạnh AC và diện tích tam giác ABC.
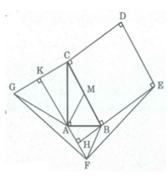
Gọi M là trung điểm của BC, ta có:
AM = MB = 1/2 BC = a (tính chất tam giác vuông)
Suy ra MA = MB = AB = a
Suy ra ∆ AMB đều ⇒ ∠ (ABC) = 60 0
Mặt khác: ∠ (ABC) + ∠ (ACB) = 90 0 (tính chất tam giác vuông)
Suy ra: ∠ (ACB) = 90 0 - ∠ (ABC) = 90 0 – 60 0 = 30 0
Trong tam giác vuông ABC, theo Pi-ta-go, ta có: B C 2 = A B 2 + A C 2
⇒ A C 2 = B C 2 - A B 2 = 4 a 2 - a 2 = 3 a 2 ⇒ AC = a 3
Vậy S A B C = 1/2 .AB.AC
= 1 2 a . a 3 = a 2 3 2 ( đ v d t )
Cho lăng trụ tam giác ABC.A’B’C’ đáy ABC là tam giác đều cạnh a, hình chiếu vuông góc H của A’ trên mặt phẳng (ABC) trùng với trực tâm của tam giác ABC. Tất cả các cạnh bên đều tạo với mặt phẳng đáy góc 60°. Thể tích của khối lăng trụ ABC.A’B’C’là:
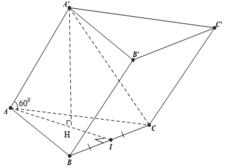
A. a 3 3 4
B. a 3 3 6
C. a 3 3 2
D. a 3 2 2
Đáp án A
Gọi I là giao điểm của AH và BC
Theo giả thiết H là trực tâm của tam giác đều ABC nên AH là đường cao và H cũng lả trọng tâm của tam giác đều ABC
