Rút gọn biểu thức:
a) x + 31 + (-12) + 52; b) (-35) - (x + 23) + 61;
c) 127- (127 - x) + 23; d) 107 - (107 + x - 23)
Rút gọn biểu thức:
a) (-37) – (x + 23) + 15 =
b) 176 – (176 - x + 42) =
c) 1270 – (1270 – 2x) + 31 =
d) 2x + (-141) – (231 – 461) =
Lời giải:
a.
$=-37-x-23+15=-x-(37+23)+15=-x-60+15=-x-(60-15)=-x-45$
b.
$=176-176+x-42=0+x-42=x-42$
c.
$=1270-1270+2x+31=0+2x+31=2x+31$
d.
$=2x-141-231+461=2x-(141+231)+461=2x-372+461$
$=2x+(461-372)=2x+89$
x+31+(-42)+52
rút gọn biểu thức
Bài 3: Rút gọn biểu thức:
| a) 2+ (- 81) -(24+ 81) c)66 -(12-x)+(12-66) | b)( -9-x+ 2) +9 d)15-(15-x+93)+93 |
giúp mình ạ
a: =2-81-24-81=-22-162=-184
a) Bạn Nguyễn Lê Phước Thịnh giải rồi nha bạn :)
b) (-9-x+2)+9
=-9-x+2+9
=-9+(-x)+2+9
=(-x)+(-9+2+9)
=(-x)+2
c) 66-(12-x)+(12-66)
=66-12+x+12-66
=x
d) 15-(15-x+93)+93
=15-15+x-93+93
=x
Bài 10: Cho biểu thức:A=3x^2+6x+12/x^3-8
a, Tìm ĐKXĐ của A
b, Rút gọn A
c, Tính giá trị của biểu thức tạix=2021/1010
\(a,ĐK:x\ne2\\ b,A=\dfrac{3\left(x^2+2x+4\right)}{\left(x-2\right)\left(x^2+2x+4\right)}=\dfrac{3}{x-2}\\ c,x=\dfrac{2021}{1010}\Leftrightarrow A=\dfrac{3}{\dfrac{2021}{1010}-\dfrac{2020}{1010}}=\dfrac{3}{\dfrac{1}{1010}}=3030\)
Rút gọn biểu thức:A=\(\dfrac{2}{\sqrt{x}+2}-\dfrac{1}{\sqrt{x}-2}+\dfrac{4}{x-4}\)
đk : x >= 0 ; x khác 4
\(A=\dfrac{2\sqrt{x}-4-\sqrt{x}-2+4}{x-4}=\dfrac{\sqrt{x}-2}{x-4}=\dfrac{1}{\sqrt{x}+2}\)
\(A=\dfrac{2}{\sqrt{x}+2}-\dfrac{1}{\sqrt{x}-2}+\dfrac{4}{x-4}\left(đk:x>2\right)\)
\(=\dfrac{2\left(\sqrt{x}-2\right)-\left(\sqrt{x}+2\right)+4}{x-4}\)
\(=\dfrac{2\sqrt{x}-4-\sqrt{x}-2+4}{x-4}=\dfrac{\sqrt{x}-2}{x-4}=\dfrac{1}{\sqrt{x}+2}\)
ĐKXĐ: x khác 4; x ≥ 0
\(A=\dfrac{2\sqrt{x}-4-\sqrt{x}-2+4}{x-4}=\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{1}{\sqrt{x}+2}\)
Bỏ dấu giá trị tuyệt đối và rút gọn biểu thức:
a) \(A=3x+2+\left|5x\right|\) trong hai trường hợp: x ≥ 0 và x < 0
b) \(B=\left|-4x\right|-2x+12\) trong hai trường hợp: x ≤ 0 và x > 0
a) Khi `x≥0`
`=> A=3x+2+5x`
`=> A=8x+2`
Khi `x<0`
`=> A=-3x+2-5x`
`=> A=-8x+2`
b) Khi `x≥0`
`=> B=-4x-2x+12`
`=> B=-6x+12`
Khi `x<0`
`=> B=4x+2x+12`
`=> B=6x+12`
cho biểu thức: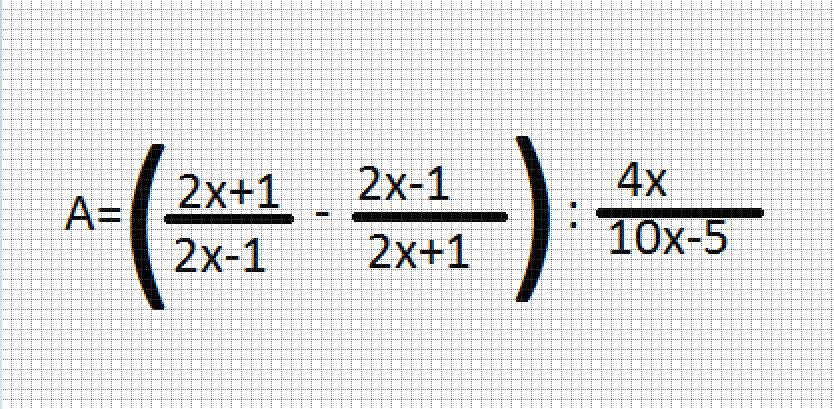
a)tìm điều kiện của x để giá trị của biểu thức A được xác định
b)rút gọn biểu thức
a: ĐKXĐ: x<>1/2; x<>-1/2; x<>0
b: \(A=\dfrac{4x^2+4x+1-4x^2+4x-1}{\left(2x-1\right)\left(2x+1\right)}\cdot\dfrac{5\left(2x-1\right)}{4x}\)
\(=\dfrac{8x}{4x}\cdot\dfrac{5}{2x+1}=\dfrac{10}{2x+1}\)
Rút gọn biểu thức:a, A=|x|-|x-5|
b,B=|x+2|+|-5+x|
Rút gọn biểu thức:
a) A=(x-y)2+(x+y)2
b) B=(2x-1)2-2(2x-3)2+4
a, \(A=\left(x-y\right)^2+\left(x+y\right)^2\)
\(=x^2-2xy+y^2+x^2+2xy+y^2\)
\(=2x^2+2y^2\)
a) \(A=\left(x-y\right)^2+\left(x+y\right)^2\\ =x^2-2xy+y^2+x^2+2xy+y^2=2x^2+2y^2\)
b) \(B=\left(2x-1\right)^2-2\left(2x-3\right)^2+4\\ =4x^2-4x+1-2\left(4x^2-12x+9\right)+4\\ =4x^2-4x+1-8x^2+24x-18+4\)
\(=-4x^2+20x-13\)