Trên hình vẽ sau:
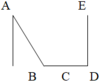
Đoạn thẳng song song với AB là ...........................
Trên hình vẽ sau:
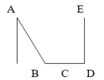
a) Đoạn thẳng song song với AB là .....................................................................................
b) Đoạn thẳng vuông góc với ED là .....................................................................................
a. Đoạn thẳng AB song song với đoạn thẳng DE
b. Đoạn thẳng ED vuông góc với đoạn thẳng DC
Trên hình vẽ sau
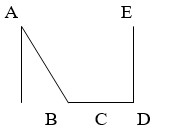
a) Đoạn thẳng song song với AB là
b) Đoạn thẳng vuông góc với ED là
Cho tam giác
ABC vuông tại A. Trên BC lấy điểm M bất kỳ. Vẽ đường thẳng qua M và song song với AB cắt AC tại N. Vẽ đường thẳng qua M và song song với AC cắt AB tại P.
a) Chứng minh MNAP là hình chữ nhật.
a: Xét tứ giác APMN có
NM//AP
MP//AN
Do đó: APMN là hình bình hành
mà \(\widehat{NAP}=90^0\)
nên APMN là hình chữ nhật
Cho tam giác ABC cân ở B( BA = BC ). Lấy điểm E trên đáy AC.Qua E vẽ đường thẳng vuông góc với AC cắt BC tại D. Từ E vẽ đường thẳng song song với BC cắt AB ở I. Đường thẳng E song song với AB cắt BC ở K.
a) Chứng minh BIEK là hình bình hành
b) Vẽ đường thẳng vuông góc với AC tại C, cắt EK tại H. Chứng minh DHCE là hình chứ nhật
c) Vẽ điểm F đối xứng E qua I. Chứng minh tam giác IBF = tam giác KHB
d) Chứng minh B là trung điểm của FH
bạn đánh có sai đề ko thế. Đề sao vô lí thế bạn "lấy điểm E trên cạnh AC . Từ E kẻ vuông góc vơi AC cắt BC tại D" lm sao vẽ được
Câu 3: Cho tam giác ABC, điểm I nằm giữa B và C. Qua I vẽ đường thẳng song song với AB, cắt AC ở H. Qua I vẽ đường thẳng song song với AC, cắt AB ở K.
a, Tứ giác AHIK là hình gì?
b/ điểm l ở vị trí nào trên BC thì tứ giác AHIK là hình thoi
c, Tam giác ABC có điều kiện gì thì tứ giác AHIK là hình chữ nhật.
a, Vì \(HI\text{//}AB;KI\text{//}AC\Rightarrow AHIK\text{ là hbh}\)
b, Để \(AHIK\) là hình thoi thì \(AI\) là phân giác \(\widehat{HIK}\)
Hay I là chân đường phân giác từ A tới BC
c, Để \(AHIK\) là hcn thì \(\widehat{HAK}=90^0\) hay \(\widehat{BAC}=90^0\)
Vậy tam giác ABC vuông tại A thì \(AHIK\) là hcn
Cho tam giác ABC, điểm I nằm giữa B và C. Qua I vẽ đường thẳng song song với AB, cắt AC ở H. Qua I vẽ đường thẳng song song với AC, cắt AB ở K. Điểm I ở vị trí nào trên BC thì tứ giác AHIK là hình thoi
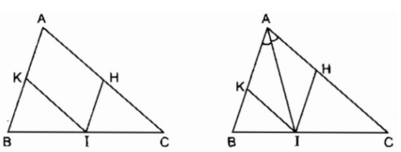
Hình bình hành AHIK là hình thoi nên đường chéo AI là phân giác của ∠ (BAC)
Ngược lại nếu AI là phân giác của ∠ (BAC) thì hình bình hành AHIK có đường chéo AI là phân giác của một góc nên hình bình hành AHIK là hình thoi.
Vậy nếu I là giao điểm của đường phân giác của ∠ A với cạnh BC thì tứ giác AHIK là hình thoi.
Nguyễn Lê Phước Thịnh66GP , Karen9GP
 huhu giúp thêm bài 11 nữa dc không ạ vẽ hình nữa nha
huhu giúp thêm bài 11 nữa dc không ạ vẽ hình nữa nha
Cho tam giác ABC vuông tại A ( AB < AC ) đường cao AH . Trên nưa r mặt phẳng bờ là dường thẳng BC có chứa điểm A , vẽ hình vuông AHKI . Gọi F là giao điểm của AC và KI . Đường thẳng qua F và song song với AB cắt đường thẳng qua B và song song với AC tại E
a ) Cho AH =2cm . Tính diện tích hình vuông AHKI
b ) Chứng minh : ABEF là hình vuông
c ) CM : HI//EK
d ) CM : 3 đường thẳng AE , BF , HI đồng qui
Nguyễn Lê Phước Thịnh66GP
Karen9GP
Cho tam giác ABC vuông tại A ( AB < AC ) đường cao AH . Trên nưa r mặt phẳng bờ là dường thẳng BC có chứa điểm A , vẽ hình vuông AHKI . Gọi F là giao điểm của AC và KI . Đường thẳng qua F và song song với AB cắt đường thẳng qua B và song song với AC tại E
a ) Cho AH =2cm . Tính diện tích hình vuông AHKI
b ) Chứng minh : ABEF là hình vuông
c ) CM : HI//EK
d ) CM : 3 đường thẳng AE , BF , HI đồng qui
a) \(S_{ẠHKI}=AH^2=4\) (cm2).
b) Áp dụng định lý Thales ta có:
\(\dfrac{AF}{AC}=\dfrac{HK}{HC}\Leftrightarrow\dfrac{AF}{AC}=\dfrac{AH}{HC}\).
Lại có: \(\Delta AHC\sim\Delta BAC\left(g.g\right)\Rightarrow\dfrac{AH}{HC}=\dfrac{BA}{AC}\).
Do đó AF = BA. Dễ dàng suy ra được ABEF là hình vuông.
c) Tứ giác FKEB nội tiếp đường tròn đường kính FB nên:
\(\widehat{EKB}=\widehat{EFB}=45^o\) (cùng chắn cung EB).
Mà \(\widehat{IHK}=45^o\) nên HI // EK.
d) Gọi X là giao điểm của BF và AE.
5 điểm F, K, E, B, A cùng thuộc đường tròn đường kính FB mà XF = XE = XA = XB nên XK = XA.
Từ đó X nằm trên đường trung trực của AK hay X nằm trên IH.
Vậy ta có đpcm.
Cách khác:
b) Xét \(\Delta AHB\) và \(\Delta AIF\) có: \(\left\{{}\begin{matrix}\widehat{AHB}=\widehat{AIF}=90^o\\\widehat{BAH}=\widehat{IAF}\left(=90^o-\widehat{FAH}\right)\\AI=AH\end{matrix}\right.\)
\(\Rightarrow\Delta AHB=\Delta AIF(g.c.g)\)
\(\Rightarrow AB=AF\).
Do đó tứ giác ABEF là hình vuông.
c) Gọi O là tâm hình vuông ABEF.
Ta có OA = OB = OE = OF.
Xét tam giác AKF vuông tại K có O là trung điểm của BF nên OK = OB = OF.
Từ đó OK = OA = OE hay tam giác AKE vuông tại K.
Lại có tứ giác AHKI là hình chữ nhật nên \(AK\perp HI\Rightarrow\) HI // EK.
c) Ta có OA = OK và HA = HK nên \(OH\perp AK\).
Lại có \(AK\perp HI\Rightarrow\) O, H, I thẳng hàng.
Vậy HI, AE, BF đồng quy tại O.