Tìm côsin góc giữa 2 đường thẳng d1: 10x+ 5y- 1=0 và d 2 : x = 2 + t y = 1 - t
A. 1 2
B. 1 10
C. 3 10
D. Tất cả sai
Tìm côsin góc giữa 2 đường thẳng d1: x+ 2y -7= 0 và d2: 2x- 4y+ 9= 0.
A. - 3 5
B. 2 5
C. 1 5
D. 3 5
Vectơ pháp tuyến của đường thẳng d1 là n1=(1;2)
Vectơ pháp tuyến của đường thẳng d2 là n2=(2;-4)
Gọi φ là góc giữa 2 đường thẳng ta có:
cos φ = n 1 . n 2 n 1 . n 2 = - 3 5
Chọn A.
Cho d1:2x+5y+4=0 và d2:5x-2y+6=0.Số đo của góc giữa 2 đường thẳng d1 và d2 là? A.90° B.60° C.45° D.30°
Tìm góc giữa 2 đường thẳng d: 6x- 5y+ 15 = 0 và ∆ 2 : x = 10 - 6 t y = 1 + 5 t .
A.900
B.300
C. 450
D. 600
Vectơ pháp tuyến của đường thẳng d là n 1 = ( 6 ; - 5 )
Vectơ pháp tuyến của đường thẳng là ∆ 2 =(5;6)
Ta có n 1 . n 2 = 0 => d ⊥ ∆ 2
Chọn A.
Côsin góc giữa 2 đường thẳng Δ1: x + 2y - 2 = 0 và Δ2: x - y = 0 là:
A. 10 10
B. 2
C. 2 3
D. 3 3
Tìm côsin góc giữa hai đường thẳng Δ1 : \(2x+y-1=0\) vaf △2 : \(\left\{{}\begin{matrix}x=2+t\\y=1-t\end{matrix}\right.\)
Đường thẳng \(\Delta_1\) nhận \(\overrightarrow{u_1}=\left(1;-2\right)\) là 1 vtcp
Đường thẳng \(\Delta_2\) nhận \(\left(1;-1\right)\) là 1 vtcp
\(\Rightarrow cos\left(\Delta_1;\Delta_2\right)=\dfrac{\left|\overrightarrow{u_1}.\overrightarrow{u_2}\right|}{\left|\overrightarrow{u_1}\right|.\left|\overrightarrow{u_2}\right|}=\dfrac{\left|1.1+\left(-2\right).\left(-1\right)\right|}{\sqrt{1^2+\left(-2\right)^2}.\sqrt{1^2+\left(-1\right)^2}}=\dfrac{3}{\sqrt{10}}\)
Tìm góc giữa hai đường thẳng (d1): x+√3+1=0 và (d2): x+10=0
Góc giữa 2 đường thẳng d1:x+3y-3=0 và d2: x+√3y +2=0
\(d_1\) nhận \(\overrightarrow{n_1}=\left(1;3\right)\) là 1 vtpt
\(d_2\) nhận \(\overrightarrow{n_2}=\left(1;\sqrt{3}\right)\) là 1 vtpt
Gọi \(\alpha\) là góc giữa d1 và d2
\(\Rightarrow cos\alpha=\left|cos\left(\overrightarrow{n_1};\overrightarrow{n_2}\right)\right|=\dfrac{\left|1.1+3.\sqrt{3}\right|}{\sqrt{1^2+3^2}.\sqrt{1^2+3}}=\dfrac{3\sqrt{3}+1}{2\sqrt{10}}\)
\(\Rightarrow\alpha\approx11^034'\)
Tìm số đo của góc giữa hai đường thẳng d1 và d2 lần lượt có phương trình: d1: 4x – 2y + 6 = 0 và d2: x – 3y + 1 = 0
Với d1: 4x – 2y + 6 = 0 có vecto pháp tuyến là: n1→(4;-2)
và d2: x – 3y + 1 = 0 có vecto pháp tuyến là: n2→(1;-3) ; ta có :
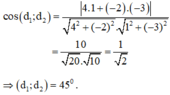
Cho hai đường thẳng d 1 : x = 2 + t y = - 1 + t z = 3 v à d 2 : x = 1 - t y = 2 z = - 2 + t . Góc giữa hai đường thẳng d1 và d2 là:
A. 30°
B. 45°
C. 90°
D. 60°
Chọn D.
Gọi u 1 → ; u 2 → lần lượt là vectơ chỉ phương của đường thẳng d1; d2.
Áp dụng công thức ta có cosin góc giữa hai đường thẳng là:
