Giải các bất phương trình lôgarit sau: log x 2 - x - 2 < 2 log 3 - x
PB
Những câu hỏi liên quan
Giải các bất phương trình lôgarit:
a) log12(8- 6x) ≥ 6;
c) log0,4x – log9(x- 4) < log0,43;
các p nhanh dùm mk nha
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giải các bất phương trình lôgarit sau: ln|x - 2| + ln|x + 4| ≤ 3ln2
ln|(x − 2)(x + 4)| ≤ ln8
⇔| x 2 + 2x − 8| ≤ 8
⇔ −8 ≤ x 2 + 2x – 8 ≤ 8
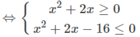
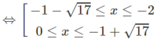
Vậy tập nghiệm là
Đúng 0
Bình luận (0)
Giải các bất phương trình lôgarit:
a) log12(8- 6x) ≥ 6;
c) log0,4x – log9(x- 4) < log0,43;
có ai pít làm ko ,nhanh lên dùm mk nha
Đúng 0
Bình luận (0)
Giải các bất phương trình lôgarit sau :
a) \(\dfrac{\ln x+2}{\ln x-1}< 0\)
b) \(\log^2_{0,2}x-\log_{0,2}x-6\le0\)
c) \(\log\left(x^2-x-2\right)< 2\log\left(3-x\right)\)
d) \(\ln\left|x-2\right|+\ln\left|x+4\right|\le3\ln2\)
H24
SGK Kết nối tri thức và cuộc sống
15 tháng 8 2023 lúc 19:33
Xét phương trình \(2{\log _2}x = - 3.\)
a) Từ phương trình trên, hãy tính \({\log _2}x.\)
b) Từ kết quả ở câu a và sử dụng định nghĩa lôgarit, hãy tìm x.
tham khảo
a)Chia cả hai vế của phương trình cho \(2\), ta được:
\(log_2x=-\dfrac{3}{2}\)
Vậy \(log_2x=-\dfrac{3}{2}\)
b) Áp dụng định nghĩa của logarit, ta có:
\(log_2x=-\dfrac{3}{2}\Leftrightarrow2^{-\dfrac{3}{2}}=x\)
Vậy \(x=\dfrac{\sqrt{2}}{4}\)
Đúng 2
Bình luận (0)
Giải các bất phương trình lôgarit sau:
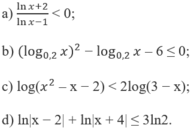
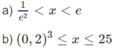
c) Bất phương trình đã cho tương đương với hệ:
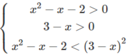
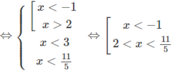
Vậy tập nghiệm là (− ∞ ; −1) ∪ (2; 11/5)
d) ln|(x − 2)(x + 4)| ≤ ln8
⇔| x 2 + 2x − 8| ≤ 8
⇔ −8 ≤ x 2 + 2x – 8 ≤ 8
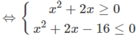
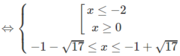
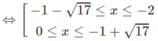
Vậy tập nghiệm là
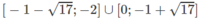
Đúng 0
Bình luận (0)
H24
SGK Kết nối tri thức và cuộc sống
20 tháng 8 2023 lúc 19:40
Giải các bất phương trình sau:
a) \({\log _2}\left( {x - 2} \right) < 2\);
b) \(\log \left( {x + 1} \right) \ge \log \left( {2x - 1} \right)\).
a, ĐK: \(x-2>0\Rightarrow x>2\)
\(log_2\left(x-2\right)< 2\\ \Leftrightarrow x-2< 4\\ \Leftrightarrow x< 6\)
Kết hợp với ĐKXĐ, ta được: \(2< x< 6\)
b, ĐK: \(2x-1>0\Leftrightarrow x>\dfrac{1}{2}\)
\(log\left(x+1\right)\ge log\left(2x-1\right)\\ \Leftrightarrow x+1\ge2x-1\\ \Leftrightarrow x\le2\)
Kết hợp với ĐKXĐ, ta được: \(\dfrac{1}{2}< x\le2\)
Đúng 0
Bình luận (0)
Giải các bất phương trình lôgarit sau: log 0 , 2 x 2 - log 0 , 2 x - 6 ≤ 0
Giải các bất phương trình lôgarit sau: lnx + 2 lnx - 1 < 0