a) Cho phân số a b ( a , b ∈ ℕ , b ≠ 0 ) .Giả sử a b <1 và m ∈ ℕ , m ≠ 0 . Chứng tỏ rằng a b < a + m b + m .
b) Áp dụng so sánh: 437 564 v à 446 573 .
Cho phân số a b a , b ∈ ℕ , b ≠ 0
Giả sử a b < 1 và m ∈ ℕ , m ≠ 0 . Chứng minh rằng: a b < a + m b + m
Thực hiện quy đồng: a b = a b + m b b + m = a b + a m b 2 + b m
a + m b + m = b a + m b b + m = a b + b m b 2 + b m
Vì a b < 1 ⇒ a < b ⇒ a b + a m < a b + b m
Từ đó ta thu được a b < a + m b + m
Cho phân số a/b (a, b ∈ N, b # 0)
Giả sử a/b<1 và m ∈ N, m ≠ 0. Chứng tỏ rằng:
a/b<a+m/b+m
giúp mình với![]()
![]()
![]()
Cho phân số a/b (a, b ∈ N, b # 0)
Giả sử a b > 1 và m ∈ N, m ≠ 0. Chứng tỏ rằng:
a b > a + m b + m
Ta có: 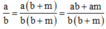
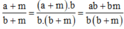
Ta có: a/b > 1 nên a > b suy ra am > bm, suy ra ab + am > ab + bm.
Do đó 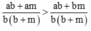
Hay 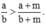
Cho phân số a/b (a, b ∈ N, b # 0)
Giả sử a b < 1 và m ∈ N, m ≠ 0. Chứng tỏ rằng:
a b < a + m b + m
Cho M = \(\dfrac{a^2+b^2}{a+b}\) (a>0, b>0, a khác b). Giả sử a, b là các số dương phân biệt thỏa mãn a + b = 2. Chứng minh rằng M > 1.
Ta có \(M=\dfrac{a^2}{a+b}+\dfrac{b^2}{a+b}\ge\dfrac{\left(a+b\right)^2}{2\left(a+b\right)}\)(BĐT Schwarz)
\(=\dfrac{a+b}{2}=1\)
"=" <=> a = b = 1 (không thỏa mãn điều kiện)
=> "=" không xảy ra => M > 1(ĐPCM)
Giả sử ∫ 1 2 1 + x 2 x 4 d x = 1 c a a - b b + c b a ; b ; c ∈ ℕ ; 1 ≤ a , b , c ≤ 9 . Tính giá trị biểu thức S = C 2 a + c b - a .
A. 165
B. 715
C. 5456
D. 35
Chọn D.
Phương pháp: Tính tích phân để suy ra a, b, c.
Cách giải: Ta có:
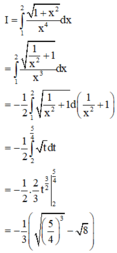
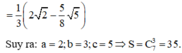
a. Cho phân số a/b (a, b thuộc N, b≠0 ). Giả sử a/b >1 và m thuộc N . Chứng tỏ rằng a/b >a+m/b?+m
Vì \(\frac{a}{b}>1\left(a,b\inℕ,b\ne0\right)\) nên \(a>b\)
\(a>b\Rightarrow a=b+n\left(n\inℕ^∗\right)\)
Ta có : \(\frac{a}{b}=\frac{b+n}{b}=1+\frac{n}{b}\) ; \(\frac{a+m}{b+m}=\frac{b+m+n}{b+m}=1+\frac{n}{b+m}\)
Mà \(\frac{n}{b}>\frac{n}{b+m}\) nên \(1+\frac{n}{b}>1+\frac{n}{b+m}\)
hay \(\frac{a}{b}>\frac{a+m}{b+m}\) (đpcm)
cho phân số a phần b, biết a, b thuộc N, b khác 0
giả sử a phần b < 1 và m thuộc N, m khác 0. chứng tỏ rằng
\(\frac{a}{b}<\frac{a+m}{b+m}\)
cho phân số a/b(a,b thuộc N , b khác 0).
giả sử a/b < 1 và m thuộc N, m khác 0.Chứng tỏ rằng:
a/b < a+m/b+m
b
áp dụng kết quả ở câu a để so sánh 434/561 và 441/568