Nghiêm của phương trình sin2 x = - sinx + 2 là:
PB
Những câu hỏi liên quan
Giải phương trình
sin
x
+
cos
x
cos
x
-
sin
x
1
+
sin
2
x
A.
x
π
/
4
+
k
π
h...
Đọc tiếp
Giải phương trình sin x + cos x cos x - sin x = 1 + sin 2 x
A. x = π / 4 + k π h o ặ c x = k π
B. x = - π / 4 + k 2 π h o ặ c x = k 2 π
C. x = - π / 4 + k π h o ặ c x = k 2 π
D. x = - π / 4 + k π h o ặ c x = k π
cho phương trình \(\dfrac{1}{sinx}+\dfrac{1}{sin2x}+\dfrac{1}{sin4x}+...+\dfrac{1}{sin2^{2018}x}=0\)
\(\dfrac{1}{sin2k}=\dfrac{sink}{sink.sin2k}=\dfrac{\left(sin2k-k\right)}{sink.sin2k}=\dfrac{sin2k.cosk-cos2k.sink}{sink.sin2k}\)
\(=\dfrac{cosk}{sink}-\dfrac{cos2k}{sin2k}=cotk-cot2k\)
Do đó pt tương đương:
\(cot\dfrac{x}{2}-cotx+cotx-cot2x+...+cot2^{2017}x-cot^{2018}x=0\)
\(\Leftrightarrow cot\dfrac{x}{2}-cot2^{2018}x=0\)
\(\Leftrightarrow\dfrac{x}{2}=2^{2018}x+k\pi\)
\(\Leftrightarrow...\)
Đúng 3
Bình luận (1)
Nghiêm của phương trình sin2x - sin x+ 2 là
Đọc tiếp
Nghiêm của phương trình sin2x = - sin x+ 2 là
1. 2cos2x + sinx = sin3x
2. cos2x + 2(sin3x-1)sin2(π/4 - x/2) = 0
1.
\(\Leftrightarrow2cos2x+sinx-sin3x=0\)
\(\Leftrightarrow2cos2x-2cos2x.sinx=0\)
\(\Leftrightarrow2cos2x\left(1-sinx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=0\\sinx=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{2}+k2\pi\\x=\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\x=\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
2.
\(cos^2x+\left(sin3x-1\right)\left(1-cos\left(\dfrac{\pi}{2}-x\right)\right)=0\)
\(\Leftrightarrow1-sin^2x+\left(sin3x-1\right)\left(1-sinx\right)=0\)
\(\Leftrightarrow\left(1-sinx\right)\left(1+sinx\right)+\left(sin3x-1\right)\left(1-sinx\right)=0\)
\(\Leftrightarrow\left(1-sinx\right)\left(1+sinx+sin3x-1\right)=0\)
\(\Leftrightarrow2\left(1-sinx\right)sin2x.cosx=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=1\\sin2x=0\\cosx=0\end{matrix}\right.\)
\(\Leftrightarrow sin2x=0\)
\(\Leftrightarrow x=\dfrac{k\pi}{2}\)
Đúng 0
Bình luận (1)
Phương trình sin2 x+ 3sinx – 40 có nghiệm là:
Đọc tiếp
Phương trình sin2 x+ 3sinx – 4=0 có nghiệm là:
Hướng dẫn giải:
Chọn A.
Đặt 
, phương trình trở thành:
Đúng 0
Bình luận (0)
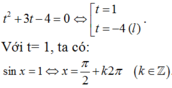
Giải phương trình sau: sin2 x + sin2x - 2 cos2 x = 1/2
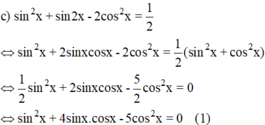
+ Xét cos x = 0 ⇒ sin2x = 1 – cos2x = 1
(1) trở thành 1 = 0 (Vô lý).
+ Xét cos x ≠ 0, chia cả hai vế cho cos2x ta được:
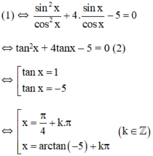
Vậy phương trình có tập nghiệm
(k ∈ Z)
Đúng 0
Bình luận (0)
Phương trình cos2x + sin2 x+ 2cosx +1 = 0 có nghiệm là
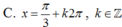
Hướng dẫn giải:
Chọn B
Ta có: cos2x + sin2x + 2cosx + 1 = 0
có 2cos2 x – 1 + 1- cos2x + 2cos x+ 1 = 0
Đúng 0
Bình luận (0)
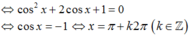
Có bao nhiêu giá trị nguyên của m để pt sin2 x - sinx - 3 -m = 0 có nghiệm duy nhất thuộc [-π/2;π/2]
Số nghiệm của phương trình
2
sin
2
2
x
+
cos
2
x
+
1
0
trong
0
;
2018
π
là A. 1008. B....
Đọc tiếp
Số nghiệm của phương trình 2 sin 2 2 x + cos 2 x + 1 = 0 trong 0 ; 2018 π là
A. 1008.
B. 2018.
C. 2017.
D. 1009.
