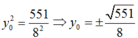Cho 4 điểm A(0; -2) ; B( -1; 0) ; C( 0; -4) và D( -2; 0) . Tìm tọa độ giao điểm của 2 đường thẳng AB và CD.
A. (1; -2)
B. (2;3)
C. vô số
D. Không có giao điểm
Trong không gian tọa độ Oxyz cho các điểm A(2; 0; 0), A’(6; 0; 0), B(0; 3; 0), B’(0 ;4; 0), C(0; 0; 4), C’(0; 0; 3).
Chứng minh rằng trực tâm H của tam giác ABC, trọng tâm G của tam giác A’B’C’ cùng nằm trên một đường thẳng đi qua O. Viết phương trình đường thẳng đó.
Tọa độ điểm \(G\) là \(G\left(\dfrac{6+0+0}{3},\dfrac{0+4+0}{3},\dfrac{0+0+3}{3}\right)\) suy ra \(G\left(2,\dfrac{4}{3},1\right)\).
\(\overrightarrow{AB}=\left(-2,3,0\right),\overrightarrow{BC}=\left(0,-3,4\right),\overrightarrow{CA}=\left(2,0,-4\right)\)
Đặt \(H\left(a,b,c\right)\).
Vì \(H\) là trực tâm tam giác \(ABC\) nên
\(\left\{{}\begin{matrix}\overrightarrow{AH}.\overrightarrow{BC}=0\\\overrightarrow{BH}.\overrightarrow{CA}=0\\\left[\overrightarrow{AB},\overrightarrow{AC}\right].\overrightarrow{AH}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3b+4c=0\\2a-4c=0\\12\left(a-2\right)+8b+6c=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{72}{61}\\b=\dfrac{48}{61}\\c=\dfrac{36}{61}\end{matrix}\right.\) suy ra \(H\left(\dfrac{72}{61},\dfrac{48}{61},\dfrac{36}{61}\right)\).
\(\overrightarrow{OG}=\left(2,\dfrac{4}{3},1\right)\)
Đường thẳng qua OG: \(\left\{{}\begin{matrix}x=2t\\y=\dfrac{4}{3}t\\z=t\end{matrix}\right.\).
Bằng cách thử trực tiếp, ta thấy H nằm trên đường thẳng OG.
Bài 1: Cho hai điểm A(1;3;5), B(1;-1;1), khi đó trung điểm I của AB có tọa độ là:
A. I(0;-4;-4).
B. I(2;2;6).
C. I(0;-2;-4).
Tọa độ trung điểm I của AB là:
\(\left\{{}\begin{matrix}x=\dfrac{1+1}{2}=1\\y=\dfrac{3-1}{2}=\dfrac{2}{2}=1\\z=\dfrac{5+1}{2}=\dfrac{6}{2}=3\end{matrix}\right.\)
vậy: I(1;1;3)
Trong mặt phẳng tọa độ Oxy, cho ba điểm A(-4; 0); B(-5; 0) và C(3; 0). Tìm điểm M thuộc trục hoành sao cho M A → + M B → + M C → = 0 → .
A. M (-2; 0)
B. M(2; 0)
C. M(- 4; 0)
D. M(- 5; 0)
Ta có M ∈ O x nên M(x;O) và M A → = − 4 − x ; 0 M B → = − 5 − x ; 0 M C → = 3 − x ; 0 ⇒ M A → + M B → + M C → = − 6 − 3 x ; 0 .
Do M A → + M B → + M C → = 0 → nên − 6 − 3 x = 0 ⇔ x = − 2 ⇒ M − 2 ; 0 .
Chọn A.
Cho hàm số f ( x ) = - 1 4 x có đồ thị (C) và các điểm M (0; 4); P (4; −1); Q (−4; 1); A (8; −2); O (0; 0). Có bao nhiêu điểm trong số các điểm trên thuộc đồ thị hàm số (C).
A. 4
B. 3
C. 2
D. 1
Lần lượt thay tọa độ các điểm M, O, P, Q, A vào hàm số f ( x ) = - 1 4 x ta được:
+) Với M (0; 4), thay x = 0; y = 4 ta được 4 = - 1 4 .0 ⇔ 4 = 0 (vô lý) nên M ∉ (C)
+) Với O (0; 0), thay x = 0 ; y = 0 ta được 0 = - 1 4 .0 ⇔ 0 = 0 (luôn đúng) nên O ∈ (C)
+) Với P (4; −1), thay x = 4 ; y = − 1 ta được −1 = - 1 4 . 4 ⇔ 1 = −1 (luôn đúng) nên P ∈ (C)
+) Với Q (−4; 1), thay x = − 4 ; y = 1 ta được 1 = - 1 4 .(−4) ⇔ 1 = 1 (luôn đúng) nên Q ∈ (C)
+) Với A (8; −2), thay x = 8 ; y = − 2 ta được −2 = - 1 4 .8 ⇔ −2 = −2 (luôn đúng) nên A ∈
Đáp án cần chọn là: A
Cho A( 0; 3) ; B( 4; 2) . Điểm D thỏa O D → + 2 D A → - 2 D B → = 0 → ,tọa độ điểm D là:
A. (2; 8)
B. (4; -8)
C. ( 8; -2)
D. đáp án khác
Trong mặt phẳng tọa độ Oxy, cho điểm A(3; 4) và hàm số y = 4/3 x .
a) Điểm A có thuộc đồ thị của hàm số y = 4/3 x hay không? Vì sao?
b) Vẽ đồ thị của hàm số y = 4/3 x .
c) Xác định các điểm H(3; 0), P(6; 0), Q(0; 4) trên mặt phẳng tọa độ Oxy ở trên.
d) Chứng minh AO = AP
a: \(y=\dfrac{4}{3}\cdot3=4\)
=>A có thuộc đồ thị
Trong mặt phẳng tọa độ Oxy, cho điểm A(3; 4) và hàm số y = 4/3 x .
a) Điểm A có thuộc đồ thị của hàm số y = 4/3 x hay không? Vì sao?
b) Vẽ đồ thị của hàm số y = 4/3 x .
c) Xác định các điểm H(3; 0), P(6; 0), Q(0; 4) trên mặt phẳng tọa độ Oxy ở trên.
d) Tam giác AOP là tam giác gì? Vì sao? Tính diện tích của tam giác AOP.
a: y=4/3x3=4
=>A có thuộc đồ thị y=4/3x
Cho elip 3x2 + 4y2 – 48 = 0 và đường thẳng d: x - 2y + 4 = 0. Giao điểm của d và Elip là
A. (0; - 4); (-2; -3) B. (4; 0); (3; 2) C. (0; 4); (-2; 3) D. (-4; 0); (2; 3)
Có: `x-2y+4=0`
`<=>x=2y-4`
Thay `x=2y-4` vào `(E)` có:
`3(2y-4)^2+4y^2-48=0`
`<=>3(4y^2-16y+16)+4y^2-48=0`
`<=>12y^2-48y+48+4y^2-48=0`
`<=>` $\left[\begin{matrix} y=3\\ y=0\end{matrix}\right.$
`@y=3=>x=2.3-4=2`
`@y=0=>x=2.0-4=-4`
`=>` Tọa độ giao điểm của `(E)` và `(d)` là: `(2;3)` và `(-4;0)`
`->D`
\(\Rightarrow\) \(chọn\) \(D\)
\(xét\) \(hpt\) \(:\)
\(\left\{{}\begin{matrix}3x^2+4y^2-48=0\\x-2y+4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3\left(2y-4\right)^2+4y^2-48=0\\x=2y-4\end{matrix}\right.\)
\(giải:\) \(3\left(4y^2-16y+16\right)+4y^2-48=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}12y^2-48y+48+4y^2-48=0\\16y^2-48y=0\\\left[{}\begin{matrix}y=0\Rightarrow x=-4\\y=3\Rightarrow x=2\end{matrix}\right.\end{matrix}\right.\)
\(vậy\) \(giao\) \(điểm\) \(của\) \(elip\) \(\left(E\right)\) \(là\) \(\left(-4;0\right)\) \(và\) \(\left(2;3\right)\)
Trong mặt phẳng Oxy, cho hai điểm F1(-4; 0) và F2(4;0) và điểm A(0; 3). Điểm M thuộc E nào sau đây thỏa MF1= 3MF2.
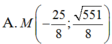
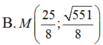
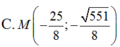
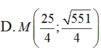
Đáp án B
- Giả sử:
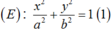
Theo giả thiết thì : c = 4 nên a2- b2= 16 (2)
(E) qua A suy ra :
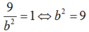
thay vào (2) ta có:
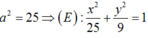
M thuộc (E)
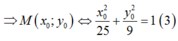
Theo tính chất của (E) ta có bán kính qua tiêu
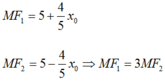
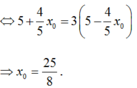
Thay vào ta có: