Kết quả sai số tuyệt đối của một phép đo là 0,0609. Số chữ số có nghĩa là:
A. 1
B. 2
C. 4
D. 3
Kết quả sai số tuyệt đối của một phép đo là 0,0609. Số chữ số có nghĩa là
A. 1.
B. 3.
C. 2.
D. 4.
Đáp án B
Chữ số có nghĩa là số đầu tiên khác 0 tính từ trái qua phải (là số 6) → tất cả có 3 chữ số có nghĩa
Kết quả sai số tuyệt đối của một phép đo là 0,0609. Số chữ số có nghĩa là:
A. 1
B. 2
C. 4
D. 3
Kế quả sai số tuyệt đối của một phép đo là 0,0609. Số chữ số có nghĩa là:
A. 1
B. 2
C. 4
D. 3
Đáp án D
Tất cả các số khác 0 là chữ số có nghĩa. Các số 0 ở giữa các số khác 0 là số có nghĩa. Các số 0 ở cuối của số thập phân có nghĩa. Các số 0 ở đầu là các số không có nghĩa. Các số 0 ở cuối các số tự nhiên không có nghĩa.
a. Sai số tuyệt đối (MAD) và sai số tỷ đối (MAPE) được tính như sau:
Phép đo thực tế (TTT): 200,1mm, 200mm, 199mm, 200,05mm, 199,05mm
Phép đo lý thuyết (TDT): 200mm, 200mm, 200mm, 200mm, 200mm, 200mm
MAD = |(TTT - TDT)| = |(200,1 - 200), (200 - 200), (199 - 200), (200,05 - 200), (199,05 - 200)| = (0,1), 0, 1, 0, 1, 1 mm
MAPE = |(TTT - TDT)/TTT)|*100 = |(200,1 - 200)/200,1), (200 - 200)/200), (199 - 200)/199), (200,05 - 200)/200,05), (199,05 - 200)/199,05)|*100 = 0,05%, 0%, 0,05%, 0,05%, 0,05%
b. Kết quả phép đo:
Độ lỗi tuyệt đối tối đa: 1,1 mm (từ 0,1 mm tới 1,1 mm)Độ lỗi tỷ đối tối đa: 0,05% (từ 0% tới 0,05%)Vậy độ lỗi tuyệt đối và tỷ đối tối đa của phép đo đo chiều dài quyển sách 5 lần là:
Độ lỗi tuyệt đối tối đa: 1,1 mmĐộ lỗi tỷ đối tối đa: 0,05%Câu 1 .Đo chiều dài một quyển sổ 5 lần được kết quả là: 200,1mm; 200mm; 199mm; 200,05mm; 199,05mm. độ chia nhỏ nhất trên thước đo là 1mm.
a. Tính sai số tuyệt đối và sai số tỷ đối của phép đo?
b. Viết kết quả phép đo?
a. Sai số tuyệt đối và sai số tỷ đối:
Ta tính tổng độ sai số của các giá trị đo lượng thực như sau:
Sai sốĐộ sai số
| 0 | 200mm |
| 0 | 200mm |
| 1 | 199mm |
| 5 | 200,05mm |
| 1 | 199,05mm |
Tổng độ sai số = 0 + 0 + 1 + 5 + 1 = 7
Giá trị thực là 550mm, vậy sai số tuyệt đối = |550 - 500| = 100.
Tỷ đối sai số = (7/1000) x 100 = 0.7%.
b. Kết quả phép đo:
Sai số tuyệt đối: 100mmSai số tỷ đối: 0.7%Vậy kết quả phép đo của chiều dài quyển sổ là 550mm với sai số tuyệt đối là 100mm và sai số tỷ đối là 0.7%.
Một học sinh làm thí nghiệm đo bước sóng của nguồn sáng bằng thí nghiệm khe Y- âng. Giá trị trung bình và sai số tuyệt đối của phép đo khoảng cách hai khe sáng là a và ∆ a . Giá trị trung bình và sai số tuyệt đối của phép đo khoảng cách chứa hai khe đến màn đo được là D và ∆ D ; giá trị trung bình và sai số tuyệt đối của phép đo khoảng vân là i và ∆ i . Kết quả sai số tương đối của phép đo bước sóng được tính bằng:
A. ε % = ∆ a a + ∆ i i - ∆ D D . 100 %
B. ε % = ∆ a + ∆ i + ∆ D . 100 %
C. ε % = ∆ a + ∆ i - ∆ D . 100 %
D. ε % = ∆ a a + ∆ i i + ∆ D D . 100 %
Đáp án D
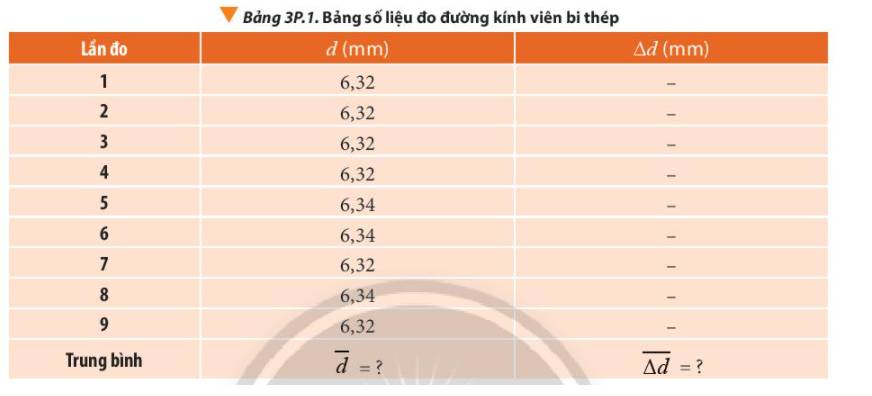
Biểu thức tính bước sóng là: λ = i D a
Nên ![]()
Kết quả sai số tuyệt đối của phép đo bước sóng được tính bằng: ε % = ∆ a a + ∆ i i + ∆ D D . 100 %
STUDY TIP
Tính sai số:
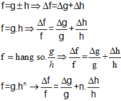
2. Bảng 3P.1 thể hiện kết quả đo đường kính của một viên bi thép bằng thước kẹp có sai số dụng cụ là 0,02 mm. Tính sai số tuyệt đối và biểu diễn kết quả phép đo có kèm theo sai số.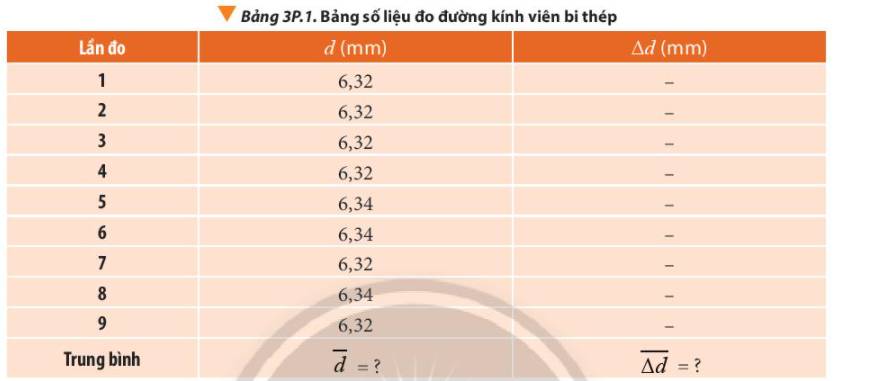
Bảng 3P.1 thể hiện kết quả đo đường kính của một viên bi thép bằng thước kẹp có sai số dụng cụ là 0,02 mm. Tính sai số tuyệt đối và biểu diễn kết quả phép đo có kèm theo sai số.
Giá trị trung bình của đường kính viên bi thép là:
\(\overline d = \frac{{{d_1} + {d_2} + ... + {d_9}}}{9} \approx 6,33(mm)\)
Sai số tuyệt đối ứng với mỗi lần đo là:
\(\begin{array}{l}\Delta {d_1} = \left| {\overline d - {d_1}} \right| = \left| {6,33 - 6,32} \right| = 0,01(mm) = \Delta {d_2} = \Delta {d_3} = \Delta {d_4} = \Delta {d_7} = \Delta {d_9}\\\Delta {d_5} = \left| {\overline d - {d_5}} \right| = \left| {6,33 - 6,34} \right| = 0,01(mm) = \Delta {d_6} = \Delta {d_8}\end{array}\)
Sai số tuyệt đối trung bình của phép đo:
\(\overline {\Delta d} = \frac{{\Delta {d_1} + \Delta {d_2} + ... + \Delta {d_9}}}{9} = 0,01(mm)\)
Sai số tuyệt đối của phép đo là:
\(\Delta d = \overline {\Delta d} + \Delta {d_{dc}} = 0,01 + 0,02 = 0,03(mm)\)
một học sinh dùng thước cặp có sai số dụng cụ 0.01mm để đo đường kính d của 1 viên bi, giá trị trung bình của n lần đo đường kính là \(\overline{d}\)=12mm và sai số tuyệt đối trung bình của n lần đo là \(\overline{\Delta d}\)=0.05mm. kết quả phép đo là