Cho đồ thị hàm số y = -x + 4. Đồ thị hàm số cắt trục Ox, Oy lần lượt tại A; B. Tính khoảng cách AB?
A. 4
B. 4 2
C. 8
D. 6 2
1) Cho hàm số bậc nhất y = (2m -1)x-4 có đồ thị là đường thẳng (d) \(\left(m\ne\dfrac{1}{2}\right)\)
a) Vẽ đồ thị hàm số
b) Tìm tọa độ giao điểm C của (d) với đồ thị hàm số \(y=3x+2\left(d_1\right)\)
2) Tìm m để (d) cắt trục Ox , Oy lần lượt tại A , B sao cho tam giác AOB cân
1: Bạn bổ sung đề bài đi bạn
2: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\\left(2m-1\right)x-4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\\left(2m-1\right)x=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{4}{2m-1}\\y=0\end{matrix}\right.\)
=>\(OA=\sqrt{\left(\dfrac{4}{2m-1}-0\right)^2+\left(0-0\right)^2}=\dfrac{4}{\left|2m-1\right|}\)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=\left(2m-1\right)x-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=\left(2m-1\right)\cdot0-4=-4\end{matrix}\right.\)
=>OB=4
Để ΔOAB cân tại O thì OA=OB
=>\(\dfrac{4}{\left|2m-1\right|}=4\)
=>\(\dfrac{1}{\left|2m-1\right|}=1\)
=>\(\left|2m-1\right|=1\)
=>\(\left[{}\begin{matrix}2m-1=1\\2m-1=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2m=2\\2m=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=1\\m=0\end{matrix}\right.\)
Cho hàm số y = mx + 2 tìm m để đồ thị hàm số cắt hai trục Ox Oy lần lượt tại A B sao cho chu vi tam giác OAB = 3 + căn 5
Để tìm m để đồ thị hàm số cắt hai trục Ox và Oy tại A và B sao cho chu vi tam giác OAB là 3 + căn 5, ta cần xác định tọa độ của A và B.
Điểm A nằm trên trục Ox, nên tọa độ của A là (x_A, 0). Thay vào phương trình hàm số y = mx + 2, ta có:
0 = mx_A + 2
=> mx_A = -2
=> x_A = -2/m
Điểm B nằm trên trục Oy, nên tọa độ của B là (0, y_B). Thay vào phương trình hàm số y = mx + 2, ta có:
y_B = m*0 + 2
=> y_B = 2
Chu vi tam giác OAB được tính bằng công thức chu vi tam giác:
chu_vi = AB + OA + OB
Với OA = x_A và OB = y_B, ta có:
chu_vi = AB + x_A + y_B
chu_vi = AB + (-2/m) + 2
chu_vi = AB - (2/m) + 2
Theo đề bài, chu vi tam giác OAB là 3 + căn 5, nên ta có:
3 + căn 5 = AB - (2/m) + 2
căn 5 = AB - (2/m) + 1
AB = căn 5 + (2/m) - 1
Ta đã có tọa độ của A và B, và chu vi tam giác OAB. Giờ ta sẽ tính độ dài AB:
AB = căn((x_A - 0)^2 + (y_B - 0)^2)
AB = căn((-2/m)^2 + 2^2)
AB = căn(4/m^2 + 4)
AB = căn(4(1/m^2 + 1))
AB = 2căn(1/m^2 + 1)
So sánh với công thức đã tính được trước đó:
AB = căn 5 + (2/m) - 1
Ta có:
2căn(1/m^2 + 1) = căn 5 + (2/m) - 1
Bình phương cả hai vế của phương trình:
4(1/m^2 + 1) = 5 + 4/m^2 + 1 - 4/m
4/m^2 + 4 = 6 + 4/m^2 - 4/m
8/m^2 = 2 - 4/m
Nhân cả hai vế của phương trình cho m^2:
8 = 2m^2 - 4
2m^2 = 12
m^2 = 6
m = ±√6
Vậy, để đồ thị hàm số cắt hai trục Ox và Oy tại A và B sao cho chu vi tam giác OAB là 3 + căn 5, ta có hai giá trị của m: √6 và -√6.
Cho đồ thị hàm số y = x + 4
b) Gọi A, B lần lượt là giao điểm của đồ thị hàm số với các trục Ox, Oy. Tính diện tích tam giác OAB ( đơn vị đo trên trục tọa độ là cm)
b) Ta có:
S A O B = 1/2 OA.OB = 1/2 |-4|.4 = 8 ( c m 2 )
a, Vẽ đồ thị hàm số y=1/2x^2
b, Cho hàm số bậc nhất y=ax-2. Hãy xác định hệ số a, biết a>0 và đồ thị hàm số cắt trục hoành Ox và truc tung Oy lần lượt tại 2 điểm A va B sao cho OB=2OA ( O là gốc tọa độ )
Cho 2 hàm số y = x và y = 0,25x.
a) Vẽ trên trên cùng 1 mặt phẳng tọa độ đồ thị của 2 hàm số đã cho.
b) Đường thẳng song song với trục Ox và cắt trục Oy tại điểm có tung độ là 4 lần lượt cắt các đường thẳng y = x và y = 0,25x tại A và B. Tìm tọa độ của các điểm A, Bvà tính chu vi, diện tích của tam giác OAB theo đơn vị đo trên các trục tọa độlà xentimét.
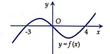
Cho đồ thị hàm số y=f(x) đi qua gốc tọa độ O, ngoài ra còn cắt trục Ox tại các điểm có hoành độ lần lượt bằng ‒3 và 4 như hình bên. Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số và trục Ox.
A. S = ∫ − 3 4 f x d x
B. S = ∫ − 3 0 f x d x + ∫ 0 4 f x d x
C. S = ∫ − 3 0 f x d x + ∫ 4 0 f x d x
D. S = ∫ 0 - 3 f x d x + ∫ 0 4 f x d x
1. Cho hai hàm số y=x và y=3x.
a) Vẽ đồ thị của hai hàm số trên cùng một hệ trục tọa độ Oxy.
b) Đường thẳng song song với trục Ox ,cắt trục Oy tại điểm có tung độ bằng 6, cắt các đồ thị trên lần lượt ở A và B. tính chu vi và diện tích tam giác OAB.
Cho hàm số: y = mx - 2m - 1 (d) (m khác 0)
Đồ thị hàm số (d) cắt trục Ox, Oy lần lượt tại A và B. Xác định m để tam giác AOB có diện tích là 4
Bài III(2 điểm) Cho hàm số y= (3m - 1)x + 4.
1) Vẽ đồ thị hàm số với m = 1
2) Tìm m để đồ thị hàm số cắt trục Ox, Oy tại 2 điểm A, B sao cho tam giác OABcó diện tích bằng 6
\(1,m=1\Leftrightarrow y=2x+4\\ 2,\text{PT giao Ox: }y=0\Leftrightarrow\left(3m-1\right)x=-4\Leftrightarrow x=\dfrac{4}{1-3m}\Leftrightarrow A\left(\dfrac{4}{1-3m};0\right)\Leftrightarrow OA=\dfrac{4}{\left|1-3m\right|}\\ \text{PT giao Oy: }x=0\Leftrightarrow y=4\Leftrightarrow B\left(0;4\right)\Leftrightarrow OB=4\\ S_{OAB}=\dfrac{1}{2}OA\cdot OB=6\\ \Leftrightarrow\dfrac{1}{2}\cdot\dfrac{4}{\left|1-3m\right|}\cdot4=6\\ \Leftrightarrow\dfrac{8}{\left|1-3m\right|}=6\\ \Leftrightarrow\left|1-3m\right|=\dfrac{4}{3}\Leftrightarrow\left[{}\begin{matrix}1-3m=\dfrac{4}{3}\\3m-1=\dfrac{4}{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=-\dfrac{1}{9}\\m=\dfrac{7}{9}\end{matrix}\right.\)