Tính tích phân 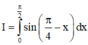A. I –1 B. I 1 C. I 0 D. I
π
4
Đọc tiếp
Tính tích phân 
A. I = –1
B. I = 1
C. I = 0
D. I = π 4
PB
Những câu hỏi liên quan
Cho hàm số yf(x) liên tục trên đoạn [0;π/3].Biết f’(x).cosx+f(x).sinx1, x ϵ [0;π/3] và f(0)1. Tính tích phân
I
∫
0
π
3
f
x
d
x
A. 1/2 + π/3 B.
3
+
1
2
C. ...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên đoạn [0;π/3].Biết f’(x).cosx+f(x).sinx=1, x ϵ [0;π/3] và f(0)=1. Tính tích phân I = ∫ 0 π 3 f x d x
A. 1/2 + π/3
B. 3 + 1 2
C. 3 - 1 2
D. 1/2
Khi đặt hiệu điện thế không đổi 30 V vào hai đầu đoạn mạch gồm điện trở thuần mắc nối tiếp với cuộn cảm thuần có độ tự cảm 1/4
π
(H) thì dòng điện trong đoạn mạch là dòng điộn một chiều có cường độ 1 A. Nếu đặt vào hai đầu đoạn mạch này điện áp xoay chiều u 150.1/
π
.cos120
π
t(V) thì biểu thức của cường độ dòng điện trong đoạn mạch là :A. i 5
2
cos(120...
Đọc tiếp
Khi đặt hiệu điện thế không đổi 30 V vào hai đầu đoạn mạch gồm điện trở thuần mắc nối tiếp với cuộn cảm thuần có độ tự cảm 1/4 π (H) thì dòng điện trong đoạn mạch là dòng điộn một chiều có cường độ 1 A. Nếu đặt vào hai đầu đoạn mạch này điện áp xoay chiều u = 150.1/ π .cos120 π t(V) thì biểu thức của cường độ dòng điện trong đoạn mạch là :
A. i = 5 2 cos(120 π t + π /4) (A).
B. i = 5 2 cos(120 π t - π /4) (A).
C. i = 5cos(120 π t - π /4) (A).
D. i = 5cos(120 π t + π /4) (A).
1 /Phân tích đa thức thành nhân tử :
x3-19x-30
2/Cho a+b+c=0. Chứng minh (a2+b2+c2) = 2(a4+b4+c4).
1. x^3-19x-30
=x^3-25x+6x-30
=x(x^2-25)+6(x-5)
=x(x+5)(x-5)+6(x-5)
=(x-5)(x^2+5x+6)
=(x-5)(x^2+2x+3x+6)
=(x-5)[x(x+2)+3(x+2)]
=(x-5)(x+2)(x+3)
Đúng 0
Bình luận (1)
2.
a + b + c = 0
<=> (a + b + c)² = 0
<=> a² + b² + c² + 2(ab + bc + ca) = 0
<=> a² + b² + c² = -2(ab + bc + ca) ------------(1)
CẦn chứng minh:
2(a^4 + b^4 + c^4) = (a² + b² + c²)²
<=> 2(a^4 + b^4 + c^4) = a^4 + b^4 + c^4 + 2(a²b² + b²c² + c²a²)
<=> a^4 + b^4 + c^4 = 2(a²b² + b²c² + c²a²)
<=> (a² + b² + c²)² = 4(a²b² + b²c² + c²a²) ---(cộng 2 vế cho 2(a²b² + b²c² + c²a²) )
<=> [-2(ab + bc + ca)]² = 4(a²b² + b²c² + c²a²) ----(do (1))
<=> 4.(a²b² + b²c² + c²a²) + 8.(ab²c + bc²a + a²bc) = 4(a²b² + b²c² + c²a²)
<=> 8.(ab²c + bc²a + a²bc) = 0
<=> 8abc.(a + b + c) = 0
<=> 0 = 0 (đúng), Vì a + b + c = 0
=> Đpcm
Đúng 0
Bình luận (1)
bài 1)
\(x^3-19x-30=x^3+2x^2-2x^2-4x-15x-30\)
=\(x^2\left(x+2\right)-2x\left(x+2\right)-15\left(x+2\right)\)
=\(\left(x+2\right)\left(x^2-2x-15\right)\)
=\(\left(x+2\right)\left(x+3\right)\left(x-5\right)\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Đặt điện áp u 100cos100
π
t(V) vào hai đầu một cuộn cảm thuần có độ tự cảm 1/2
π
(H). Biểu thức cường độ dòng điện qua cuộn cảm làA. i 2cos(100
π
t -
π
/2) (A).B. i 2cos(100
π
t +
π
/2) (A).C. i 2
2
cos(100
π
t -
π
/2) (A).D. i...
Đọc tiếp
Đặt điện áp u = 100cos100 π t(V) vào hai đầu một cuộn cảm thuần có độ tự cảm 1/2 π (H). Biểu thức cường độ dòng điện qua cuộn cảm là
A. i = 2cos(100 π t - π /2) (A).
B. i = 2cos(100 π t + π /2) (A).
C. i = 2 2 cos(100 π t - π /2) (A).
D. i = 2 2 cos(100 π t + π /2) (A).
Chọn câu đúng.
Đoạn mạch có R, L, C mắc nối tiếp có R = 40Ω, 1/C.ω = 20Ω, ωL = 60Ω. Đặt vào hai đầu mạch điện áp u = 240√2cos100πt (V). Cường độ dòng điện tức thời trong mạch là:
A. i = 3√2cos100πt (A) B. 6cos(100πt + π/4) (A)
C. i = 3√2 cos(100πt – π/4) (A) D. 6cos(100πt – π/4) (A)
Đáp án: D
Ta có: ZL = 60Ω; ZC = 20Ω
Tổng trở của mạch:
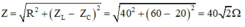
Biểu thức của i:
Ta có: u = 240√2cos100πt (V) → i = I0cos(100πt + φi)
Với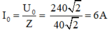 
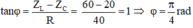
→ φ = φu – φi → φi = φu – φ = 0 – π/4 = – π/4 rad
Vậy i = 6cos(100πt – π/4) (A)
Đúng 0
Bình luận (0)
Đặt điện áp xoay chiều u 100
2
cos100πt (V) vào hai đầu một tụ điện có điện dung 2.
10
-
4
/
π
(F).Biểu thức cường độ dòng điện qua tụ điện là :A. i 2cos(100
π
t -
π
/2) (A).B. i 2
2
cos(100
π
t + ...
Đọc tiếp
Đặt điện áp xoay chiều u = 100 2 cos100πt (V) vào hai đầu một tụ điện có điện dung 2. 10 - 4 / π (F).
Biểu thức cường độ dòng điện qua tụ điện là :
A. i = 2cos(100 π t - π /2) (A).
B. i = 2 2 cos(100 π t + π /2) (A).
C. i = 2cos(100 π t + π /2) (A).
D. i = 2 2 cos(100 π t - π /2) (A).
1) Viết mỗi tập hợp sau bằng cách liệt kê các phần tử
a) A { x thuộc N / x m x ( m +1 ) với m 0 ; 1 ; 2 ; 3 ; 4
b) B { x thuộc N / 2 x m với m 0 ; 1 ; 2 ; 3 ; 4 ; 5
c) C { x thuộc N / x 3 x a - 2 với a 0 ; 1 ; 3 ; 5 ; 7
d) D { x thuộc N / x m x n x n với n 0 ; 1 ; 2 ; 3 ; 4
giúp mink với mink đang cần gấp lắm luôn
ai làm nhanh mà đúng mink tick cho
Đọc tiếp
1) Viết mỗi tập hợp sau bằng cách liệt kê các phần tử
a) A = { x thuộc N / x = m x ( m +1 ) với m = 0 ; 1 ; 2 ; 3 ; 4
b) B = { x thuộc N / 2 x m với m = 0 ; 1 ; 2 ; 3 ; 4 ; 5
c) C = { x thuộc N / x = 3 x a - 2 với a = 0 ; 1 ; 3 ; 5 ; 7
d) D = { x thuộc N / x = m x n x n với n = 0 ; 1 ; 2 ; 3 ; 4
giúp mink với mink đang cần gấp lắm luôn
ai làm nhanh mà đúng mink tick cho
khó quá
xin lỗi nhé mik ko làm đc
Đúng 0
Bình luận (1)
Xem thêm câu trả lời
Câu 18 . Phát biểu nào sau đây là sai ?A. sqrt{2} ∈ I B. sqrt{9} ∈ I C. π ∈ I D. sqrt{4} ∈ Q
Đọc tiếp
Câu 18 . Phát biểu nào sau đây là sai ?
A. \(\sqrt{2}\) ∈ I B. \(\sqrt{9}\) ∈ I C. π ∈ I D. \(\sqrt{4}\) ∈ Q
Tích phân I = ∫ 0 α x sin x d x với α ∈ [0; π] là:
A. αcosα - sinα
B. αcosα + sinα
C. -αcosα + sinα
D. -αcosα - sinα
Chọn C
Áp dụng công thức tích phân từng phần ta có:
Đúng 0
Bình luận (0)
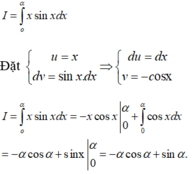
( Mu4-42. Cho hàm so $f(x)$ có đạo hàm trên đoạn $[0 ; 1]$ thỏa mãn $f(1)=0$ và $\int_0^1\left[f^{\prime}(x)\right]^2 d x=\int_0^1(x+1) e^x f(x) d x=\frac{e^2-1}{4}$. Tinh tich phân $I=\int_{0}^1 f(x) d x$.
A. $I=2-e$.
B. $I=\frac{e}{2}$.
C. $l=e-2$.
D. $1=\frac{e-1}{2}$
