Cho tam giác ABC, trong đó BC = 11cm, ∠ A B C = 38 ° , ∠ A C B = 30 ° . Gọi điểm N là chân của đường vuông góc kẻ từ A đến cạnh BC. Hãy tính:
a) Đoạn thẳng AN
b) Cạnh AC
Gợi ý: Kẻ BK vuông góc với AC.
Cho tam giác ABC vuông tại A. Gọi BC = a, AC = b, AB = c. Giải tam giác ABC, biết rằng:
a, c =3,8 cm, B ^ = 51 0
b, a = 11cm, C ^ = 60 0
Cho tam giác ABC cân tại A và AB = 5cm và BC = 6cm. Khi đó chu vi tam giác là:
A. 22cm B. 16cm C. 17cm D. 11cm
Cho tam giác ABC,trong đó BC=11cm,góc ABC=\(38^o\),góc ACB=\(30^o\).Gọi điểm N là chân của đường vuông góc kẻ từ A đến cạnh BC.Hãy tính:
a)Đoạn thẳng AN
b)Cạnh AC
(Kẻ BK trong tam giác ABC vuông góc với AC)
a: ΔANB vuông tại N
=>tan B=AN/NB
=>AN=NB*tan38
ΔANC vuông tại N
=>AN=NC*tan30
=>NB*tan38=NC*tan30
=>NB/NC=tan30/tan38\(\simeq0,74\)
=>NB=0,74NC
mà NB+NC=11
nên \(NB\simeq4,68\left(cm\right);NC\simeq6,32\left(cm\right)\)
AN=NC*tan30=6,32*tan30\(\simeq3,65\left(cm\right)\)
b: góc BAC=180-38-30=180-68=112 độ
Xét ΔABC có BC/sinA=AC/sinB
=>\(AC=\dfrac{11}{sin112}\cdot sin38\simeq7,3\left(cm\right)\)
Cho tam giác ABC trong đó BC = 11cm , góc ABC =38 độ góc ACB= 30 độ gọi điểm N là chân của đường vuông góc kẻ từ A đến cạnh BC . Hãy tính đoạn thẳng AN và cạnh AC
kẻ BK vuongAC ^CBK vuong tai K và ^C = 30 độ = > tam giácCBK nửa đều BK = BC/2 = 5,5 ^KBC = 180-(BKA+^C) = 60độ ^KBA = ^KBC-^ABC = 22 độ = >tam giác KBA có KBA = 22 độ = >AB = BK:sinKBA = 5,5:sin22 = 5,93194 AN = AB.sinABN = 3,65207 b) AC = 2AN = 7,30414
Kẻ \(BK\perp AC\left(K\in AC\right)\)
Trong tam giác vuông BKC có:
\(\widehat{KBC}=60^o-30^o=60^o\)
\(\Rightarrow\widehat{KBA}=60^o-38^o=22^o\)
BC = 11 (cm) => BK = 5,5 (cm) ( tính chất cạnh đối diện góc 30° trong tam giác vuông bằng nửa cạnh huyền )
Xét tam giác ABK vuông tại K : \(\cos KBA=\frac{BK}{AB}\)
\(\Rightarrow AB=\frac{BK}{\cos KBA}=\frac{5,5}{\cos22^o}\approx5,93\left(cm\right)\)
Xét tam giác ANB vuông tại N : \(\sin ABN=\frac{AN}{AB}\)
\(\Rightarrow AN=AB\sin ABN=5,93.\sin38^o\approx3,65\left(cm\right)\)
b) Xét tam giác ANC vuông tại N : \(\sin ACN=\frac{AN}{AC}\)
\(AC=\frac{AN}{\sin ACN}\approx\frac{3,65}{\sin30^o}\approx7,3\left(cm\right)\)
Trong tam giác ABC có AB = 11cm, ABC = ; ACB = , N là chân đường vuông góc kẻ từ A đến BC. Hãy tính AN, AC. tính S tam giác ABC.
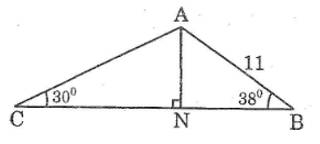
Trong tam giác vuông \(\text{ABN}\) ta có
\(\text{AN = AB.sinB}\) \(\text{= 11.sin38° ≈ 6,772 (cm)}\)
Trong tam giác vuông \(\text{ACN }\)ta có
\(\text{AC =}\) \(\dfrac{\text{AN}}{\text{sin}\widehat{\text{C}}}\) \(\approx\) \(\dfrac{\text{6,772}}{\text{sin30}^{\text{o}}}\) \(\text{= 13,544 ( cm )}\)
Trong tam giác ABC có AB = 11cm, ABC = ; ACB = , N là chân đường vuông góc kẻ từ A đến BC. Hãy tính AN, AC, diện tích ABC
góc BAC=180-38-30=150 độ-38 độ=112 độ
Xét ΔABC có
AB/sin C=AC/sin B=BC/sin A
=>11/sin 30=AC/sin 38=BC/sin112
=>\(AC\simeq13,54\left(m\right);BC\simeq20,4\left(m\right)\)
Xét ΔANB vuông tại N có
\(AN=AB\cdot sinB\)
=>\(AN=11\cdot sin38\simeq6,77\left(m\right)\)
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinA=\dfrac{1}{2}\cdot13.54\cdot11\cdot sin112\simeq69,05\left(m^2\right)\)
Cho tam giác ABC, trong đó \(BC=11cm,\widehat{ABC}=38^0,\widehat{ACB}=30^0\). Gọi điểm N là chân của đường vuông góc kẻ từ A đến cạnh BC. Hãy tính :
a) Đoạn thẳng AN
b) Cạnh AC
Gợi ý : Kẻ BK vuông góc với AC
a) Kẻ
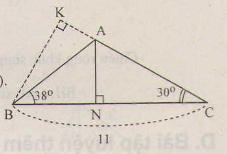
Ta được: và
Xét tam giác KBC vuông tại K có:
Xét tam giác KBA vuông tại K có:
Xét tam giác ABN vuông tại N có:
b) Xét tam giác ANC vuông tại N có
Trong tam giác ABC có AB = 11cm, ∠ ABC = 38 ° ; ∠ ACB = 30 ° , N là chân đường vuông góc kẻ từ A đến BC. Hãy tính AN, AC
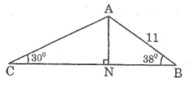
Trong tam giác vuông ABN, ta có:
AN = AB.sinB
= 11.sin 38 ° ≈ 6,772 (cm)
Trong tam giác vuông ACN, ta có:
AC = 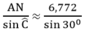
= 13,544 (cm)