Chứng minh rằng hàm số:
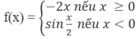
Không có đạo hàm tại x = 0 nhưng đạt cực đại tại điểm đó.
PB
Những câu hỏi liên quan
Chứng minh rằng hàm số:
f
x
-
2
x
nếu
x
≥
0
sin...
Đọc tiếp
Chứng minh rằng hàm số:
f x = - 2 x nếu x ≥ 0 sin x 2 nếu x < 0
Không có đạo hàm tại x = 0 nhưng đạt cực đại tại điểm đó.
Hàm số:
f
x
=
-
2
x
nếu
x
≥
0
sin
x
2
nếu
x
<
0
Không có đạo hàm tại x = 0 vì:
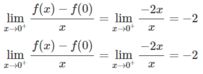
Mặt khác, với x < 0 thì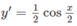 
với x > 0 thì y’ = -2 < 0
Bảng biến thiên:
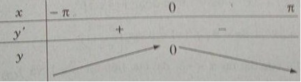
Từ đó ta thấy hàm số đạt cực đại tại x = 0 và y CD = y(0) = 0.
Đúng 0
Bình luận (0)
Chứng minh hàm số y = √|x| không có đạo hàm tại x = 0 nhưng vẫn đạt được cực tiểu tại điểm đó.
Hàm số có tập xác định D = R và liên tục trên R.
+ Chứng minh hàm số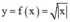 
không có đạo hàm tại x = 0.
Xét giới hạn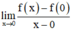 
:
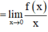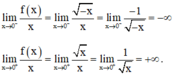
⇒ Không tồn tại giới hạn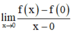 
Hay hàm số không có đạo hàm tại x = 0.
+ Chứng minh hàm số đạt cực tiểu tại x = 0 (Dựa theo định nghĩa).
Ta có : f(x) > 0 = f(0) với ∀ x ∈ (-1 ; 1) và x ≠ 0
⇒ Hàm số y = f(x) đạt cực tiểu tại x = 0.
Đúng 0
Bình luận (0)
Chứng minh rằng hàm số \(y=\sqrt{|x|}\) không có đạo hàm tại \(x=0
\) nhưng vẫn đạt cực tiểu tại điểm đó
Đặt . Giả sử x > 0, ta có :
Do đó hàm số không có đạo hàm tại x = 0 . Tuy nhiên hàm số đạt cực tiểu tại x = 0 vì .
Đúng 0
Bình luận (0)
Chứng minh hàm số y = |x| không có đạo hàm tại x = 0. Hàm số có đạt cực trị tại điểm đó không ?
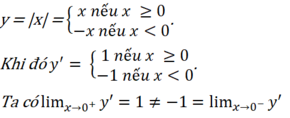
Vậy không tồn tại đạo hàm của hàm số tại x = 0.
Nhưng dựa vào đồ thị của hàm số y = |x|. Ta có hàm số đạt cực trị tại x = 0.
Đúng 0
Bình luận (0)
Chứng minh rằng hàm số :
\(f\left(x\right)=\left\{{}\begin{matrix}-2x;\left(x\ge0\right)\\\dfrac{\sin x}{2};\left(x< 0\right)\end{matrix}\right.\)
không có đạo hàm tại \(x=0\) nhưng đạt cực đại tại điểm đó.
Chứng minh rằng hàm số:
f
x
x
-
1
2
n
ế
u
x
≥
0...
Đọc tiếp
Chứng minh rằng hàm số:
f x = x - 1 2 n ế u x ≥ 0 - x 2 n ế u x < 0
Không có đạo hàm tại điểm x = 0 nhưng có đạo hàm tại điểm x = 2 .
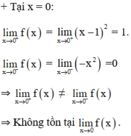
⇒ Không tồn tại đạo hàm của f(x) tại x = 0.
Đúng 0
Bình luận (0)
Xét các khẳng định sau i) Nếu hàm số yf(x) có đạo hàm cấp hai trên R và đạt cực tiểu tại
x
x
0
thì
f
x
0
0
f...
Đọc tiếp
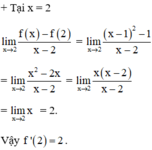
Xét các khẳng định sau
i) Nếu hàm số y=f(x) có đạo hàm cấp hai trên R và đạt cực tiểu tại x = x 0 thì f ' x 0 = 0 f ' ' x 0 > 0
ii) Nếu hàm số y=f(x) có đạo hàm cấp hai trên R và đạt cực đại tại x = x 0 thì f ' x 0 = 0 f ' ' x 0 < 0
iii) Nếu hàm số y=f(x) có đạo hàm cấp hai trên R và f ' ' x 0 = 0 thì hàm số không đạt cực trị tại x = x 0
Số khẳng định đúng trong các khẳng định trên là
A. 0
B. 1
C. 2
D. 3
H24
SGK Cánh Diều
13 tháng 8 2023 lúc 22:24
Đề bài
Chứng minh rằng hàm số \(f(x) = \left| x \right|\) không có đạo hàm tại điểm \({x_0} = 0\), nhưng có đạo hàm tại mọi điểm \(x \ne 0\)
\(y = \left| x \right| = \left\{ \begin{array}{l}x\,\,\,(x \ge 0)\\ - x\,\,\,(x < 0)\end{array} \right. \Rightarrow y' = \left\{ \begin{array}{l}1\,\,\,(x \ge 0)\\ - 1\,\,\,(x < 0)\end{array} \right.\)
Ta có: \(\mathop {\lim }\limits_{x \to {0^ + }} y' = 1 \ne - 1 = \mathop {\lim }\limits_{x \to {0^ - }} y'\)
Vậy không tồn tại đạo hàm của hàm số tại x = 0
Đúng 0
Bình luận (0)
Cho hàm số liên tục trên khoảng (a;b) và
x
0
∈
a
;
b
. Có bao nhiêu mệnh đề đúng trong các mệnh đề sau ?(1) Hàm số đạt cực trị tại điểm
x
0
khi và chỉ khi
f
x
0
0
(2) Nếu hàm số...
Đọc tiếp
Cho hàm số liên tục trên khoảng (a;b) và x 0 ∈ a ; b . Có bao nhiêu mệnh đề đúng trong các mệnh đề sau ?
(1) Hàm số đạt cực trị tại điểm x 0 khi và chỉ khi f ' x 0 = 0
(2) Nếu hàm số y = f(x) có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thỏa mãn điều kiện f ' x 0 = f " x 0 = 0 thì điểm x 0 không là điểm cực trị của hàm số y = f x
(3) Nếu f'(x) đổi dấu khi x qua điểm x 0 thì điểm x 0 là điểm cực tiểu của hàm số y = f(x)
(4) Nếu hàm số y = f(x) có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thỏa mãn điều kiện f ' x 0 = 0 , f " x 0 > 0 thì điểm x 0 là điểm cực đại của hàm số y = f(x)
A. 1
B. 2
C. 0
D. 3
