Viết các biểu thức dưới dạng bình phương của một tổng hoặc hiệu:
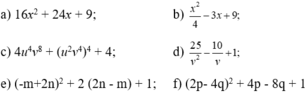
Viết các biểu thức sau đây dưới dạng bình phương của một tổng hoặc một hiệu:
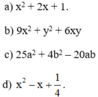
a) x2 + 2x + 1
= x2 + 2.x.1 + 12
= (x + 1)2 (Áp dụng hằng đẳng thức (1) với A = x và B = 1)
b) 9x2 + y2 + 6xy
= 9x2 + 6xy + y2
= (3x)2 + 2.3x.y + y2
= (3x + y)2 (Áp dụng hằng đẳng thức (1) với A = 3x và B = y)
c) 25a2 + 4b2 – 20ab
= 25a2 – 20ab + 4b2
= (5a)2 – 2.5a.2b + (2b)2
= (5a – 2b)2 (Áp dụng hằng đẳng thức (2) với A = 5a và B = 2b)
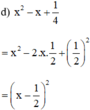
(Áp dụng hằng đẳng thức (2) với A = x và B = 1/2 )
Viết lại biểu thức sau dưới dạng bình phương của một tổng hoặc hiệu:
4x4 - 4x2 + 1
Viết các biểu thức dưới dạng bình phương của 1 tổng hoặc 1 hiệu :
m3+9m2n+27mn2+27n3
Sửa yêu cầu đề: "bình phương" \(\rightarrow\) "lập phương"
\(m^3+9m^2n+27mn^2+27n^3=\left(m+3n\right)^3\)
Viết các biểu thức dưới dạng bình phương của 1 tổng hoặc 1 hiệu :
8u3-48u2v+96uv3-64v3
viết các biểu thức dưới dạng bình phương tổng hoặc 1 hiệu: \(9x^2-6x+1\)
C1: 9x2 - 6x + 1
= (3x)2 - 3x.2.1 + 12
= (3x - 1)2
C2: 9x2 - 6x + 1
= 9x2 - 3x - 3x + 1
= 3x(3x - 1) - (3x - 1)
= (3x - 1)(3x - 1)
= (3x - 1)2
Viết các biểu thức sau dưới dạng lập phương của một tổng hoặc một hiệu
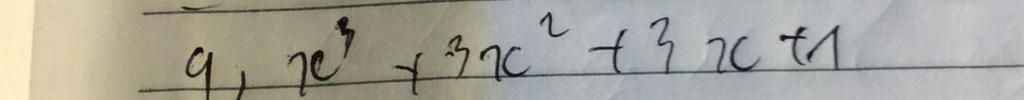
HĐT số 4: \(\left(A+B\right)^3=A^3+3A^2B+3AB^2+B^3\)
__________
\(x^3+3x^2+3x+1\)
\(=x^3+3\cdot x^2\cdot1+3\cdot x\cdot1^2+1^3\)
\(=\left(x+1\right)^3\)
`x^3 +3x^2+3x+1`
`= x^3 + 3*x^2*1 +3*x*1^2 +1^3`
`=(x+1)^3`
x^3 + 3x^2 + 3x + 1
<=> x^3 + 3x^2.1 + 3x.1^2 + 1^3
<=> (x + 1) ^3
Viết biểu thức dưới dạng bình phương của một tổng hoặc một hiệu
25a^2+4b^2-20ab
25a^2+4b^2-20ab=(5a)^2-2.5a.2b+(2b)^2
=(5a-2b)^2
25a^2+4b^2-20ab=(2b)^2-2*2b*5a+(5a)^2=(2b-5a)^2
Viết các đa thức sau dưới dạng bình phương của một tổng hoặc hiệu
4x2 + 4x + 1
\(4x^2+4x+1\)
\(=\left(2x\right)^2+2\cdot2x\cdot1+1^2\)
\(=\left(2x+1\right)^2\)
Viết các biểu thức sau dưới dạng bình phương của 1 tổng hoặc 1 hiệu: x^2-x+1/4
\(x^2-x+\frac{1}{4}\)
\(=x^2-2\cdot\frac{1}{2}\cdot x+\left(\frac{1}{2}\right)^2\)
\(=\left(x-\frac{1}{2}\right)^2\)