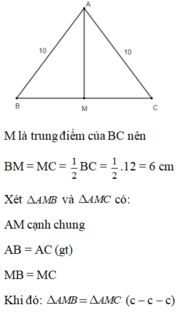
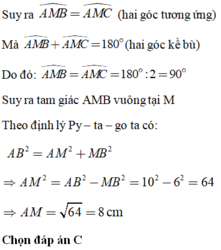Cho tam giác ABC cân tại A có AB =10cm, BC = 12cm. Gọi M là trung điểm của BC. Tính độ dài AM.
PB
Những câu hỏi liên quan
cho tam giác ABC cân tại A, M là trung điểm của BC. CMR: a, tam giác AMB= tam giác AMC. b, tính độ dài AM biết AB=10cm; BC=12cm c, kẻ đường trung tuyến CE cắt AM tại D. gọi I là điểm cách đều 3 cạnh của tam giác ABC. CMR: I;D;M thẳng hàng.
a: Xet ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
b: Ta có: ΔABC cân tại A
mà AM là trung tuyến
nên AM là đường cao
BC=12cm nên BM=6cm
=>AM=8(cm)
c: I cách đều ba cạnh nên I là giao điểm của ba đường phân giác
=>AI là phân giác của góc BAC
mà AM là phân giác của góc BC
nên A,I,M thẳng hàng
Đúng 3
Bình luận (0)
Cho tam giác ABC cân. Biết AB = AC = 10cm, BC = 12cm. M là trung điểm BC. Độ dài trung tuyến AM là:
A. 22cm.
B. 4cm.
C. 8cm.
D. 6cm.
Cho tam giác ABC cân tại A. Vẽ trung tuyến AM của tam giác. Biết B C = 12 c m , A B = A C = 10 c m thì độ dài AM là:
A. 22cm
B. 4cm
C. 8cm
D. 10cm
Tam giác ABC cân tại A, AM là đường trung tuyến đồng thời là đường cao.
Có BM = BC/2 = 6cm
Áp dụng định lí Pytago trong tam giác vuông ABM có:
AM2 = AB2 - BM2 = 102 - 62 = 64 ⇒ AM = 8m. Chọn C
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại A, BC = 10cm. Độ dài đường trung tuyến AM bằng 12cm. Khi đó độ dài AB là
A. 12cm
B. 13cm
C. 11cm
D. 10cm
Do tam giác ABC cân tại A nên AM là đường trung tuyến đồng thời là đường cao. BM=1/2 BC=5cm
Áp dụng định lí Pytago trong tam giác ABM ta có:
AB2 = BC2 + BM2 = 122 + 52 = 169 ⇒ AB = 13cm. Chọn B
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A có AB=AC=10cm, BC=12cm.
a)Gọi M là trung điểm của BC. C/minh tam giác AMB= tam giác AMC.
b) Tính AM.
c) Vẽ BK vuông góc AC, CF vuông góc AB. C/minh BK=CF và AK=AF.
Cho tam giác ABC vuông tại a có ab 6cm BC 10cm a tính độ dài cạnh ac và so sánh các góc của tam giác ABC b trên tia đối của tia ab lấy điểm d sao cho ab ad gọi k là trung điểm của BC đường thẳng dk cắt ac tại m chứng minh BC BD và tính độ dài cạnh am
Xem chi tiết
Cho tam giác ABC cân tại A. Gọi M là trung điểm của BC. Biết AB = 13, AM = 12. Tính độ dài cạnh BC
Lời giải:
Xét tam giác $ABM$ và $ACM$ có:
$AB=AC$ (do $ABC$ cân tại $A$)
$AM$ chung
$BM=CM$ (do $M$ là trung điểm $BC$)
$\Rightarrow \triangle ABM=\triangle ACM$ (c.c.c)
$\Rightarrow \widehat{AMB}=\widehat{AMC}$
Mà $\widehat{AMB}+\widehat{AMC}=180^0$ nên $\widehat{AMB}=\widehat{AMC}+90^0$
$\Rightarrow AM\perp BC$
Xét tam giác $ABM$ vuông tại $M$, áp dụng định lý Pitago:
$BM=\sqrt{AB^2-AM^2}=\sqrt{13^2-12^2}=5$
$BC=2BM=2.5=10$
Đúng 2
Bình luận (0)
Cho tam giác ABC cân có ABAC10cm, BC12cm. Kẻ AH vuông góc BC tại Ha, Chứng minh A là trung điểm của BC và tính độ dài BCb, Trên tia đối của tia BC lấy điểm M, trên tia đối của tia BC lấy điểm N sao cho BMBN. Chứng minh rằng tam giác AMN cân c, Từ B kẻ BE vuông góc AM tại E, từ C kẻ EF vuông góc AN tại F. chứng minh tam giác MBE tam giác NCFd, Gọi K là giao điểm của BE và CF. Chứng minh A,H,K thảng hàng
Đọc tiếp
Cho tam giác ABC cân có AB=AC=10cm, BC=12cm. Kẻ AH vuông góc BC tại H
a, Chứng minh A là trung điểm của BC và tính độ dài BC
b, Trên tia đối của tia BC lấy điểm M, trên tia đối của tia BC lấy điểm N sao cho BM=BN. Chứng minh rằng tam giác AMN cân
c, Từ B kẻ BE vuông góc AM tại E, từ C kẻ EF vuông góc AN tại F. chứng minh tam giác MBE= tam giác NCF
d, Gọi K là giao điểm của BE và CF. Chứng minh A,H,K thảng hàng
Cho tam giác ABC cân có ABAC10cm, BC12cm. Kẻ AH vuông góc BC tại Ha, Chứng minh A là trung điểm của BC và tính độ dài BCb, Trên tia đối của tia BC lấy điểm M, trên tia đối của tia BC lấy điểm N sao cho BMBN. Chứng minh rằng tam giác AMN cân c, Từ B kẻ BE vuông góc AM tại E, từ C kẻ EF vuông góc AN tại F. chứng minh tam giác MBE tam giác NCFd, Gọi K là giao điểm của BE và CF. Chứng minh A,H,K thảng hàng
Đọc tiếp
Cho tam giác ABC cân có AB=AC=10cm, BC=12cm. Kẻ AH vuông góc BC tại H
a, Chứng minh A là trung điểm của BC và tính độ dài BC
b, Trên tia đối của tia BC lấy điểm M, trên tia đối của tia BC lấy điểm N sao cho BM=BN. Chứng minh rằng tam giác AMN cân
c, Từ B kẻ BE vuông góc AM tại E, từ C kẻ EF vuông góc AN tại F. chứng minh tam giác MBE= tam giác NCF
d, Gọi K là giao điểm của BE và CF. Chứng minh A,H,K thảng hàng