cho tam giác ABC nếu đường thẳng m song song với BC và cắt cạnh AB thì
Cho tam giác ABC .CMR:
a.Nếu đường thẳng m song song với cạnh BC thì m sẽ cắt các đường thẳng AB,AC.
b.Nếu đường thẳng m song song với cạnh BC và cắt cạnh AB thì m sẽ cắt cạnh AC.
a) Giả sử m không cắt AB, AC. Thật vậy ta suy ra m // AB và m // AC. Suy ra AB // AC // BC (mâu thuẫn với giả thiết ABC là tam giác). Vậy ta có đpcm.
b) Giả sử m không cắt AC. Thật vậy ta suy ra m // AC. Suy ra AC // BC (mâu thuẫn với giả thiết ABC là tam giác). Vậy ta có đpcm.
CHO TAM GIÁC ABC. NẾU ĐƯỜNG THẲNG M SONG SONG VỚI CẠNH BC VÀ CẮT CẠNH AB THÌ:
A. M VUÔNG GÓC VỚI AC
B. M CẮT CẠNH AC
C. M SONG SONG AC
D. M NẰM NGOÀI TAM GIÁC ABC
Cho một tam giác ABC. Chứng minh rằng: nếu đường thẳng d song song với cạnh AB và cắt cạnh AC thì sẽ cắt cạnh BC.
Cho tam giác ABC và một điểm M nằm trên cạnh BC. Qua M ta kẻ đường thẳng song song với cạnh AB, cắt cạnh AC tại điểm E và đường thẳng song song với cạnh AC, cắt cạnh AB tại điểm D. Khi điểm M di chuyển trên cạnh BC thì trung điểm I của đoạn thẳng DE di chuyển trên đường nào?
Chứng minh được ADME là hình bình hành Þ I là trung điểm của AM. Tương tự 2A. I thuộc đường trung bình của D ABC (đường thẳng đi qua trung điểm của AB và AC)
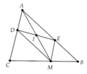
Cho tam giác ABC có đường cao AH trọng tâm G. Một đường thẳng đi qua G và song song với BC cắt các cạnh AB, AC tại M và N. Nếu diện tích tam giác ABC bằng 36 cm2 thì diện tích tam giác HMN bằng ... cm2
Cho tam giác ABC vuông tại A. Điểm I là trung điểm của cạnh BC. Qua I kẻ đường thẳng song song với AB cắt AC tại N và kẻ đường thẳng song song với AC cắt AB tại M. Tam giác ABC có thêm điều kiện gì thì AMIN là hình vuông
cho tam giác ABC có đường cao AH trọng tâm G một đường thẳng đi qua G và song song với BC . Cắt các cạnh AB, AC tại M và N .Nếu diện tích tam giác ABC bằng 36 cm2 thì diện tích tam giác HMN bằng
Cho tam giác ABC, điểm M thuộc cạnh BC sao cho M B M C = 1 2 . Đường thẳng đi qua M và song song với AC cắt AB ở D. Đường thẳng đi qua M và song song với AB cắt AC ở E. Biết chu vi tam giác ABC bằng 30cm. Chu vi của các tam giác DBM và EMC lần lượt là
A. 10cm; 15cm
B. 12cm; 16cm
C. 20cm; 10cm
D. 10cm; 20cm
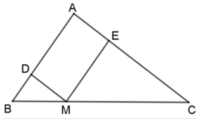
Ta có: MD // AC nên ΔDBM ~ ΔABC. Suy ra :
D B A B = B M B C = D M A C = D B + B M + D M A B + B C + C A
Do đó 1 3 = P B D M P A B C
Chu vi ΔDBM bằng 30. 1 3 = 10cm
Ta có ME // AB nên ΔEMC ~ ΔABC. Suy ra
E M A B = M C B C = E C A C = E M + M C + E C A B + B C + A C
do đó 2 3 = P E M C P A B C
Chu vi ΔEMC bằng 30. 2 3 = 20 cm
Vậy chu vi ΔDBM và chu vi ΔEMC lần lượt là 10cm; 20cm
Đáp án: D
Cho tam giác ABC, điểm M thuộc cạnh BC sao cho MB/MC=1/2.
Đường thẳng đi qua M và song song với AC cắt AB ở D. Đường thẳng đi qua M và song song với AB cắt AC ở E. Biết chu vi tam giác ABC bằng 24cm, tính chu vi của các tam giác DBM và EMC.
Ta có: \(\dfrac{MB}{MC}=\dfrac{1}{2}\)(gt)
nên MC=2MB
Ta có: MB+MC=BC(M nằm giữa B và C)
nên BC=2MB+MB=3MB
hay \(\dfrac{MB}{BC}=\dfrac{1}{3}\)
Xét ΔABC có
M∈BC(gt)
D∈AB(gt)
MD//AC(gt)
Do đó: ΔBMD\(\sim\)ΔBCA(Định lí tam giác đồng dạng)
⇒\(\dfrac{C_{BMD}}{C_{BCA}}=\dfrac{BM}{BC}\)(Tỉ số chu vi giữa hai tam giác đồng dạng)
\(\Leftrightarrow\dfrac{C_{BMD}}{24}=\dfrac{1}{3}\)
hay \(C_{DBM}=8\left(cm\right)\)
Ta có: \(\dfrac{MB}{MC}=\dfrac{1}{2}\)(gt)
nên \(MB=\dfrac{1}{2}MC\)
Ta có: MB+MC=BC(M nằm giữa B và C)
nên \(BC=\dfrac{1}{2}MC+MC=\dfrac{3}{2}MC\)
hay \(\dfrac{MC}{BC}=\dfrac{2}{3}\)
Xét ΔCBA có
M∈BC(gt)
E∈CA(Gt)
ME//AB(gt)
Do đó: ΔCME∼ΔCBA(Định lí tam giác đồng dạng)
\(\Leftrightarrow\dfrac{C_{CME}}{C_{CBA}}=\dfrac{CM}{CB}\)(Tỉ số chu vi giữa hai tam giác đồng dạng)
⇔\(\dfrac{C_{CME}}{24}=\dfrac{2}{3}\)
hay \(C_{CME}=\dfrac{48}{3}=16\left(cm\right)\)
Vậy: \(C_{DBM}=8\left(cm\right)\); \(C_{CME}=16\left(cm\right)\)