Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi E, F lần lượt là trung điểm của AB và SC; I, J lần lượt là giao điểm của AF và EF với mặt phẳng (SBD). Tỉ số IJ/JB bằng:
A. 2/3
B. 1/3
C. 1/4
D. 1/2
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi E, F lần lượt là trung điểm của AB và SC; I, J lần lượt là giao điểm của AF và EF với mặt phẳng (SBD). Tỉ số IA/IF bằng:
A. 1
B. 2
C. 3
D. 4
Trong mặt phẳng (SAC) : AF ∩S O = I là trọng tâm tam giác SBD ⇒ IA/IF=2
Đáp án B
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi E, F lần lượt là trung điểm của AB và SC; I, J lần lượt là giao điểm của AF và EF với mặt phẳng (SBD). Tỉ số EJ/IF bằng
A. 2
B. 1
C. 2/3
D. 3/4
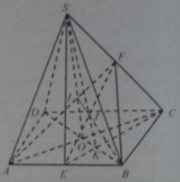
Trong mặt phẳng (ABCD) : BD ∩ EC = K
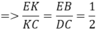
Trong mặt phẳng (SEC) : EF ∩ SK = J. Áp dụng định lí Me-nê-la-uýt vào tam giác EFC ta được: EJ/JF = 1
Đáp án B
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O, hai điểm M, N lần lượt là trung điểm của SB, SD; điểm P thuộc SC và không là trung điểm của SC. Gọi E là giao điểm của SO và MN; Q là giao điểm của SA và PE. Gọi F, G, H lần lượt là giao điểm của QM và AB, QP và AC, QN và AD. Tìm khẳng định đúng?
A. F nằm giữa G và H
B. 3 điểm F; G; H không thẳng hàng
C. G nằm giữa F và H
D. Tất cả sai
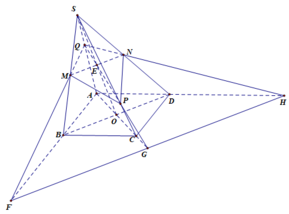
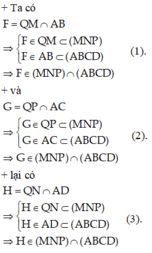
Từ (1) (2) và (3) suy ra ba điểm F, G, H thuộc giao tuyến của hai mặt phẳng (MNP) và (ABCD).
Do đó ba điểm F, G, H thẳng hàng và G nằm giữa F và H.
Chọn C.
Cho hình chóp S.ABCD thể tích V với đáy là hình bình hành. Gọi E,F lần lượt là trung điểm của các cạnh AB và AD . Thể tích của khối chóp S.AECF là
A. V 2
B. V 4
C. V 3
Cho hình chóp S.ABCD thể tích V với đáy ABCD là hình bình hành. Gọi E, F lần lượt là trung điểm của các cạnh AB và AD. Thể tích của khối chóp là
A . V 2
B . V 4
C . V 3
D . V 5
Đáp án A
Dễ thấy SAEC = 1 2 SABC = 1 4 SABCD
=> SAECF = 1 2 SABCD
VS.AECF = 1 2 VS.ABC
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi O là giao điểm của AC và BD. Gọi M, N lần lượt là trung điểm của SB, SC. Tính tỉ số thể tích giữa hai khối chóp O.BCNM và S.ABCD.
Tự vẽ hình nhé!
Ta có:
\(V_{OBCNM}=\dfrac{1}{3}d\left(O;\left(BCNM\right)\right).S_{BCNM}=\dfrac{1}{3}.\dfrac{1}{2}d\left(A;\left(SBC\right)\right).\dfrac{3}{4}S_{SBC}=\dfrac{1}{8}V_{SABC}=\dfrac{1}{16}V_{SABCD}\)
\(\Rightarrow\dfrac{V_{OBCNM}}{V_{SABCD}}=\dfrac{1}{16}\)
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Gọi \(O\) là giao điểm của \(AC\) và \(BD\); \(M,N\) lần lượt là trung điểm của \(SB,SD\); \(P\) thuộc đoạn \(SC\) và không là trung điểm của \(SC\).
a) Tìm giao điểm \(E\) của đường thẳng \(SO\) và mặt phẳng \(\left( {MNP} \right)\).
b) Tìm giao điểm \(Q\) của đường thẳng \(SA\) và mặt phẳng \(\left( {MNP} \right)\).
c) Gọi \(I,J,K\) lần lượt là giao điểm của \(QM\) và \(AB\), \(QP\) và \(AC\), \(QN\) và \(A{\rm{D}}\). Chứng minh \(I,J,K\) thẳng hàng.
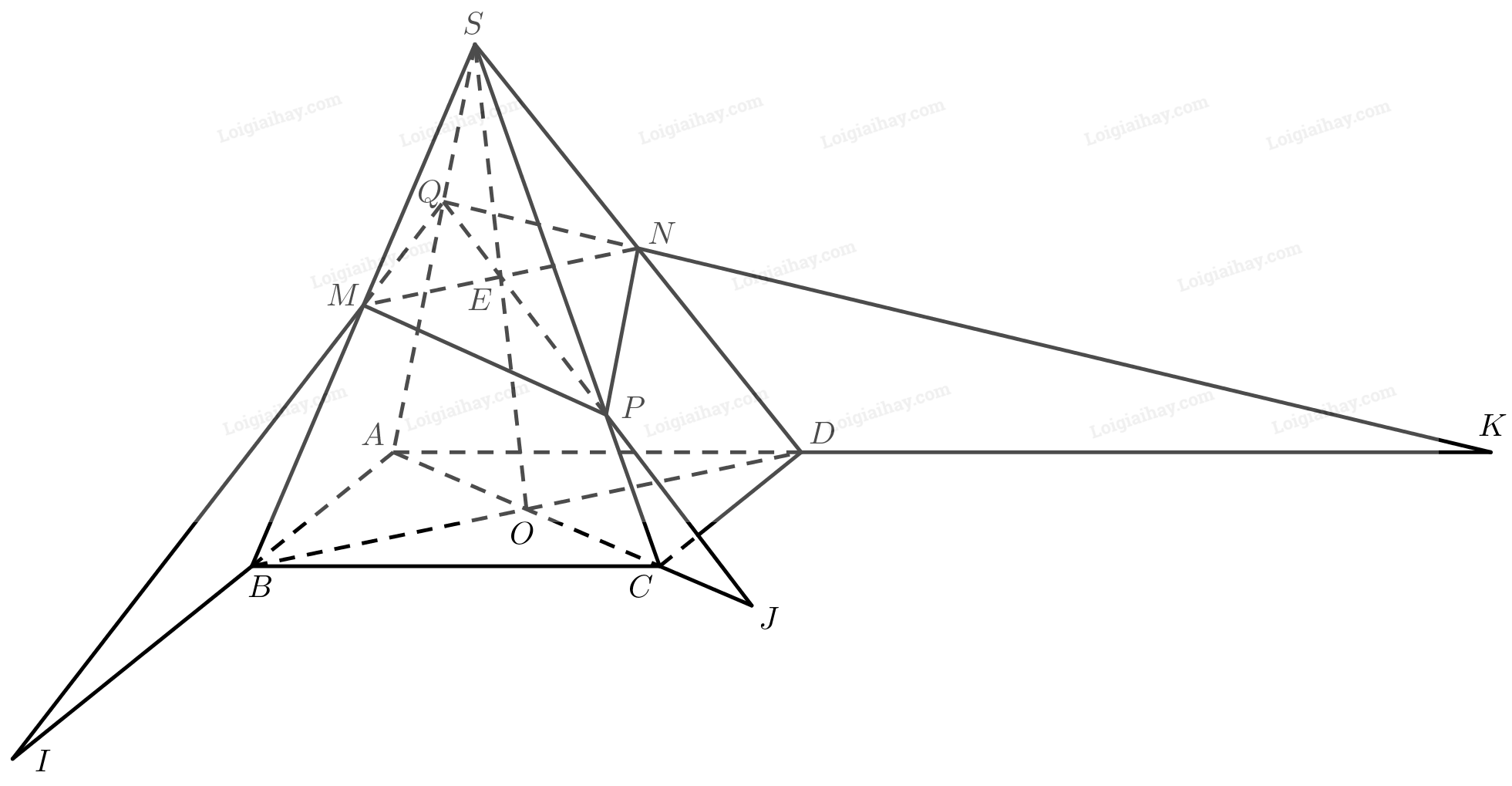
a) Gọi \(E\) là giao điểm của \(SO\) và \(MN\). Ta có:
\(\left. \begin{array}{l}E \in MN \subset \left( {MNP} \right)\\E \in S{\rm{O}}\end{array} \right\} \Rightarrow E = S{\rm{O}} \cap \left( {MNP} \right)\)
b) Gọi \(Q\) là giao điểm của \(SA\) và \(EP\). Ta có:
\(\left. \begin{array}{l}Q \in EP \subset \left( {MNP} \right)\\Q \in S{\rm{A}}\end{array} \right\} \Rightarrow Q = S{\rm{A}} \cap \left( {MNP} \right)\)
c) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}I \in QM \subset \left( {MNP} \right)\\I \in AB \subset \left( {ABC{\rm{D}}} \right)\end{array} \right\} \Rightarrow I \in \left( {MNP} \right) \cap \left( {ABCD} \right)\\\left. \begin{array}{l}J \in QP \subset \left( {MNP} \right)\\J \in AC \subset \left( {ABC{\rm{D}}} \right)\end{array} \right\} \Rightarrow J \in \left( {MNP} \right) \cap \left( {ABCD} \right)\\\left. \begin{array}{l}K \in QN \subset \left( {MNP} \right)\\K \in AD \subset \left( {ABC{\rm{D}}} \right)\end{array} \right\} \Rightarrow K \in \left( {MNP} \right) \cap \left( {ABCD} \right)\end{array}\)
Do đó, \(I,J,K\) cùng nằm trên giao tuyến của hai mặt phẳng \(\left( {MNP} \right)\) và \(\left( {ABCD} \right)\).
Vậy \(I,J,K\) thẳng hàng.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, J, E, F lần lượt là trung điểm SA, SB, SC, SD. Trong các đường thẳng sau, đường thẳng nào không song song với IJ?
A. EF
B. CD
C. AD
D. AB
Chọn C.
+) Ta có, IJ là đường trung bình tam giác SAB nên IJ // AB. ⇒ D đúng.
+) ABCD là hình bình hành nên AB// CD. Mà IJ// AB
Suy ra , IJ // CD ⇒ B đúng.
+) EF là đường trung bình tam giác SCD nên EF // CD.
Suy ra, IJ // EF ⇒ A. đúng.
- Do đó chọn đáp án C.
Bài này biểu diễn ngược hơi mệt xíu, cộng trừ mấy lần mới ra:
Gọi O là tâm đáy thì \(\overrightarrow{SO}=\dfrac{1}{2}\overrightarrow{SA}+\dfrac{1}{2}\overrightarrow{SC}=\dfrac{1}{2}\overrightarrow{SB}+\dfrac{1}{2}\overrightarrow{SD}\) (1)
\(\Rightarrow\overrightarrow{SA}+\overrightarrow{SC}=\overrightarrow{SB}+\overrightarrow{SD}\) (2)
Bây giờ tìm cách đưa \(\overrightarrow{SA};\overrightarrow{SB};\overrightarrow{SC};\overrightarrow{SD}\) biểu diễn qua \(\overrightarrow{SM};\overrightarrow{SN};\overrightarrow{SG}\) là được
Với \(\overrightarrow{SB};\overrightarrow{SD}\) đơn giản: \(\overrightarrow{SB}+\overrightarrow{SD}=2\overrightarrow{SO}=3\overrightarrow{SG}\)
\(\overrightarrow{SA}=\overrightarrow{SM}+\overrightarrow{MA}=\overrightarrow{SM}+\overrightarrow{ON}=\overrightarrow{SM}+\overrightarrow{OS}+\overrightarrow{SN}=\overrightarrow{SM}-\dfrac{3}{2}\overrightarrow{SG}+\overrightarrow{SN}\)
Đặt \(\overrightarrow{SC}=x.\overrightarrow{SH}\)
Thế vào (2):
\(\Rightarrow\overrightarrow{SM}-\dfrac{3}{2}\overrightarrow{SG}+\overrightarrow{SN}+x.\overrightarrow{SH}=3\overrightarrow{SG}\)
\(\Rightarrow\overrightarrow{SM}=\dfrac{9}{2}\overrightarrow{SG}-\overrightarrow{SN}-x.\overrightarrow{SH}\)