Chu vi của hình vuông ABCD là:
A. 20cm
B. 10cm
C. 16cm
D. 25cm
PB
Những câu hỏi liên quan
Chu vi hình vuông có cạnh 5 cm là:
a. 10cm
b. 15cm
c. 20cm
d. 25cm
Chu vi hình vuông bằng: 5 x 4 = 20 (cm)
Chọn c. 20 cm
Đúng 0
Bình luận (0)
cho hình vuông ABCD có cạnh là A= 5cm diện tích hình vuông ABC bằng bao nhiêu
A. 5cm B. 10cm C.20cm D.25cm
Xem thêm câu trả lời
Một hình vuông có chu vi bằng chu vi của hình chữ nhật có chiều dài 6cm,chiều rộng 4cm. Diện tích của hình vuông đó là :
A. 16cm2 B. 36cm2 C. 25cm2. D. 20cm2
Giải
Chu vi hình vuông là:
(6+4)x2=20 (cm)
Cạnh của hình vuông là:
20:4=5 (cm)
Diện tích hình vuông đó là:
5x5=25 (cm2)
Đáp số: 25 cm2
Vậy đáp án đúng là C.25 cm2
Đúng 0
Bình luận (0)
Chu vi hình chữ nhật là : ( 6+4)x2=20(cm)
Vì chu vi hình vuông bằng chu vi hình chữ nhật => Chu vi hình vuông là 20cm
=> Cạnh hình vuông là : 20:4= 5( cm )
=> Diện tích hình vuông là : 5x5=25(cm2)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho hình thang vuông ABCD (A = D = 90 ∘ ) có AB = 16cm, CD = 25cm, BD = 20cm. Độ dài cạnh BC là
A. 10cm
B. 12cm
C. 15cm
D. 9cm
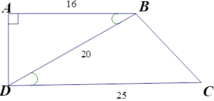
Vì ΔABD ~ ΔBDC (cmt) nên góc A = DBC.
Ta có A = 90 ∘ nên DBC = 90 ∘ . Theo định lí Pytago, ta có
B C 2 = C D 2 - B D 2 = 25 2 - 20 2 = 152 . Vậy BC = 15cm
Đáp án: C
Đúng 0
Bình luận (0)
Cho hình bình hành có độ dài hai cạnh là 10cm và 6cm. Chu vi hình bình hành là :A. 16cm B. 60cm C. 32 cm D. 68cm Hình bình hành ABCD có chu vi là 80cm, độ dài cạnh AB 25 cm . Vậy độ dài BC là A. 15 cm C. 40Cm C. 55cm D. 28cm
Đọc tiếp
Cho hình bình hành có độ dài hai cạnh là 10cm và 6cm. Chu vi hình bình hành là :
A. 16cm B. 60cm
C. 32 cm D. 68cm
Hình bình hành ABCD có chu vi là 80cm, độ dài cạnh AB = 25 cm . Vậy độ dài BC là
A. 15 cm C. 40Cm
C. 55cm D. 28cm
Bài 2 : Cho hình bình hành ABCD, có đường chéo lớn AC. Từ C kẻ CE vuông góc AB, CF vuông góc AD ; BH vuông góc AC. Chứng minh : a) AB.AE = AH.AC b) BC.AF = AC.HC c) AB.AE + AD.AF = AC2 . d) Cho biết CE = 16cm, CF = 20cm, chu vi ABCD = 108cm. Tính diện tích ABCD
Giúp mk vs khó quá
Dựng BG ⊥ AC.
Xét ∆ BGA và ∆ CEA, ta có:
ˆBGA=ˆCEA=90∘BGA^=CEA^=90∘
ˆAA^ chung
Suy ra: ∆ BGA đồng dạng ∆ CEA (g.g)
Suy ra: ABAC=AGAEABAC=AGAE
Suy ra: AB.AE = AC.AG (1)
Xét ∆ BGC và ∆ CFA, ta có:
ˆBGC=ˆCFA=90∘;BGC^=CFA^=90∘
ˆBCG=ˆCAF;BCG^=CAF^ (so le trong vì AD // BC)
Suy ra: ∆ BGC đồng dạng ∆ CFA (g.g)
Suy ra: AFCG=ACBC⇒BC.AF=AC.CGAFCG=ACBC⇒BC.AF=AC.CG
Mà BC = AD (tính chất hình bình hành )
Suy ra: AD.AF = AC.CG (2)
Cộng từng vế của đẳng thức (1) và (2) ta có:
AB.AE + AD.AF = AC.AG + AC.CG
⇒AB.AE+AD.AF=AC(AG+CG)⇒AB.AE+AD.AF=AC(AG+CG)
Mà AG+CG=ACAG+CG=AC nên AB.AE+AD.AF=AC2
Đúng 2
Bình luận (0)
Tính chu vi của các hình sau :
a) Hình tam giác có độ dài các cạch là 15cm,20cm,25cm
b) Hình tứ giác có độ dài các cạnh là 12cm , 14cm, 16cm , 18cm
a,chu vi của hình tam giác là :
15 + 20 + 25 = 60 ( cm )
đáp số : 60 cm
b, chu vi của hình tứ giác là :
12 + 14 + 16 + 18 = 60 ( cm )
đáp số : 60 cm
Đúng 2
Bình luận (0)
a) Chu vi của tam giác đó là
15+20+25=60 (cm)
Đáp số: 60 cm
b) Chu vi của tứ giác đó là
12+14+16+18=60 (cm)
Đáp số: 60cm
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
tính chu vi của các hình sau:
a) Hình tam giác có độ dài các cạnh là 15cm, 20cm, 25cm.
b) Hình tứ giác có độ dài các cạnh là 12cm, 14cm, 16cm, 18.
a) Chu vi của tam giác đó là:
15+20+25=60(cm)
đ/s
b)Chu vi của hình tứ giác là:
12+14+16+18=60(cm)
đ/s
lớp 4 mà 0 biết làm bài này là ngu đấy
a, chu vi hình tam giác là: 15 + 20 + 25= 60(cm)
b, chu vi hình tứ giác là: 12 + 14 + 16 + 18 =60(cm)
Cho hình thang vuông ABCD (A = D = 90 ∘ ) có AB = 16cm, CD = 25cm, BD = 20cm. Tam giác ABD đồng dạng với tam giác nào dưới đây?
A. ΔBDC
B. ΔCBD
C. ΔBCD
D. ΔDCB
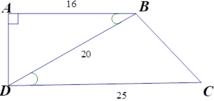
ΔABD và ΔBDC có góc ABD = BDC (hai góc ở vị trí so le trong bằng nhau do AB // CD);
Và A B B D = B D D C (vì 16 20 = 20 25 )
Do đó ΔABD ~ ΔBDC (c.g.c)
Đáp án: A
Đúng 0
Bình luận (0)
Hình thang vuông ABCD có góc A và góc D = 90 độ, AB II CD. Cho AD= 7cm, AC= 20cm, DC= 16cm. Tính chu vi hình thang đó.
áp dụng định lý pytago vào tam giác ACD
suy ra AD^2=AC^2-DC^2
suy ra AD=12
từ B kẻ đg vuông góc xuống AD cắt AD tại H
suy ra tứ giác ABHD là hình chữ nhật
suy ra AB=DH=7 suy ra CH=16-7=9
và AD=BH=12
áp dụng định lý pytago vào tam giác BHC
suy ra BC^2=BH^2+CH^2
suy ra BC=15
suy ra chu vi= 12+7+16+15=50
Đúng 0
Bình luận (0)