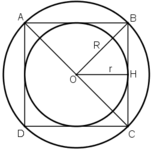
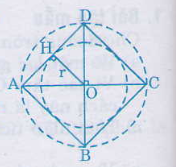
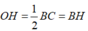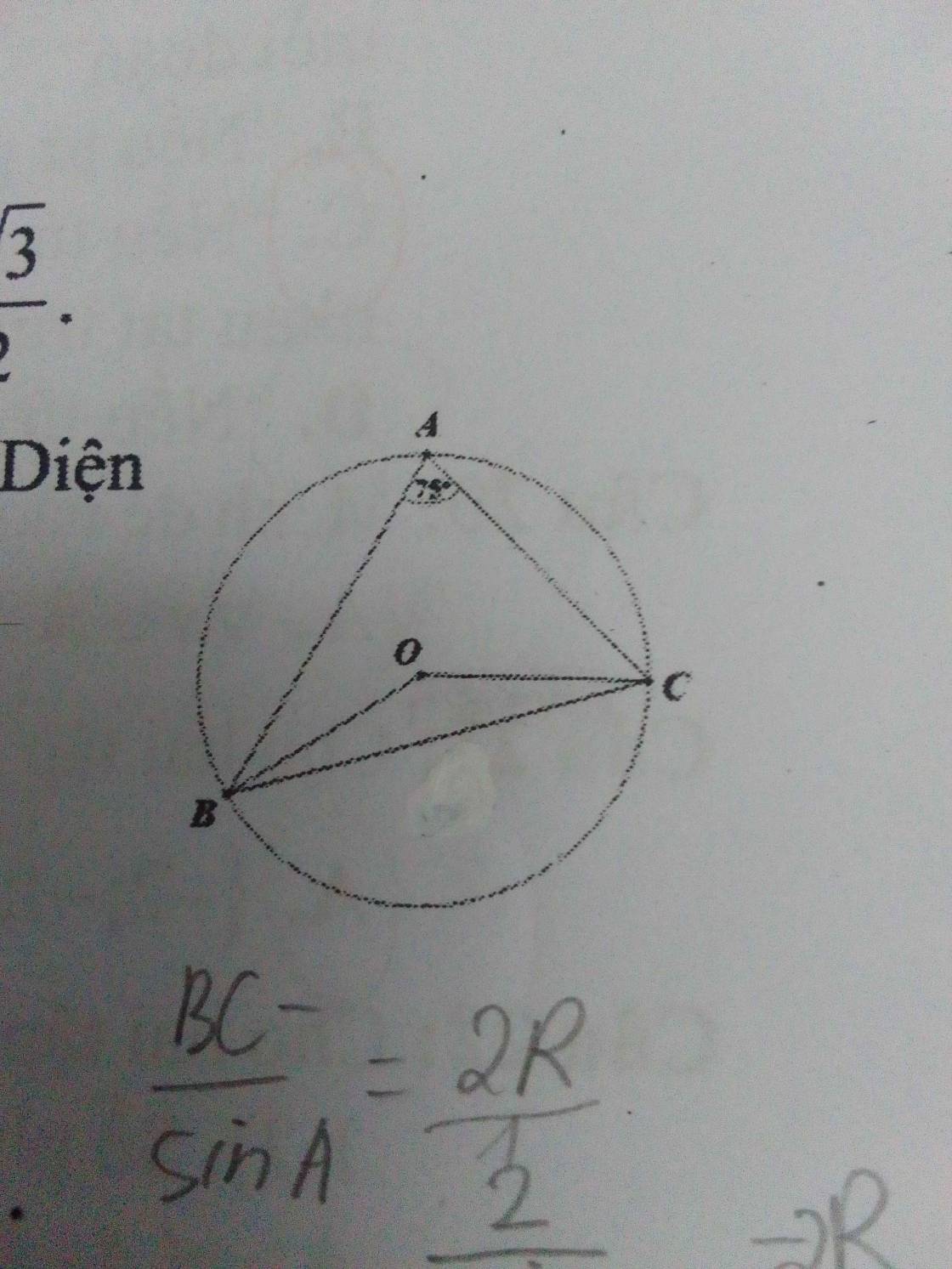Cho nội tiếp trong đường tròn tâm O, bán kính R có B A C ^ = 75 o ; A C B ^ = 60 o . Kẻ BH vuông góc với AC. Quay ∆ A B C quanh AC thì ∆ B H C tạo thành hình nón tròn xoay. Tính diện tích xung quanh của hình nón tròn xoay này
A. S x q = πR 2 3 2 3 - 1 2
B. S x q = πR 2 3 2 3 + 1 2
C. S x q = πR 2 3 4 3 - 1 2
D. S x q = πR 2 3 4 3 + 1 2