Cho ba số a, b và c đôi một phân biệt. Giải phương trình x a - b a - c + x b - a b - c + z c - a c - b = 2
PB
Những câu hỏi liên quan
Cho a,b,c là các số thực dương phân biệt có tổng bằng 3. Chứng minh rằng trong ba phương trình \(x^2-2ax+b=0;x^2-2bx+c;x^2-2cx+a=0\)
có ít nhất một phương trình có hai nghiệm phân biệt và ít nhất một phương trình vô nghiệm
* Giả sử cả 3 pt đều có nghiệm kép hoặc vô nghiệm ta có :
pt \(x^2-2ax+b=0\) (1) có \(\Delta_1'=\left(-a\right)^2-b=a^2-b\le0\)
pt \(x^2-2bx+c=0\) (2) có \(\Delta_2'=\left(-b\right)^2-c=b^2-c\le0\)
pt \(x^2-2cx+a=0\) (3) có \(\Delta_3'=\left(-c\right)^2-a=c^2-a\le0\)
\(\Rightarrow\)\(\Delta_1'+\Delta_2'+\Delta_3'=\left(a^2+b^2+c^2\right)-\left(a+b+c\right)\le0\) (*)
Lại có : \(0< a,b,c< 3\)\(\Rightarrow\)\(\hept{\begin{cases}a\left(3-a\right)>0\\b\left(3-b\right)>0\\c\left(3-c\right)>0\end{cases}\Leftrightarrow\hept{\begin{cases}3a>a^2\\3b>b^2\\3c>c^2\end{cases}}}\)
\(\Rightarrow\)\(\left(a^2+b^2+c^2\right)-\left(a+b+c\right)< 3\left(a+b+c\right)-\left(a+b+c\right)=2\left(a+b+c\right)=6>0\)
trái với (*)
Vậy có ít nhất một phương trình có hai nghiệm phân biệt
cái kia chưa bt làm -_-
Đúng 1
Bình luận (0)
nhầm r >_< sửa lại chỗ này nhé
Lại có : \(0< a,b,c< 3\)\(\Rightarrow\)\(\hept{\begin{cases}a\left(3-a\right)< 0\\b\left(3-b\right)< 0\\c\left(3-c\right)< 0\end{cases}\Leftrightarrow\hept{\begin{cases}3a< a^2\\3b< b^2\\3c< c^2\end{cases}}}\)
\(\Rightarrow\)\(\left(a^2+b^2+c^2\right)-\left(a+b+c\right)>3\left(a+b+c\right)-\left(a+b+c\right)=6>0\) :))
Đúng 1
Bình luận (0)
Cho ba số a,b và c đôi một phân biệt.Giai phương trình.
\(\frac{x}{\left(a-b\right)\left(a-c\right)}+\frac{x}{\left(b-a\right)\left(b-c\right)}\frac{x}{\left(c-a\right)\left(c-b\right)}=2\)
Cho ba số phân biệt a,b,c \(\in\) R. Chứng minh rằng phương trình:
\(\left(x-a\right)\left(x-b\right)+\left(x-b\right)\left(x-c\right)+\left(x-c\right)\left(x-a\right)=0\) luôn có hai nghiệm phân biệt
Cho ba số phân biệt a,b,c \(\in\) R. Chứng minh rằng phương trình:
\(\left(x-a\right)\left(x-b\right)+\left(x-b\right)\left(x-c\right)+\left(x-c\right)\left(x-a\right)=0\) luôn có hai nghiệm phân biệt
Đặt \(f\left(x\right)=\left(x-a\right)\left(x-b\right)+\left(x-b\right)\left(x-c\right)+\left(x-c\right)\left(x-a\right)\)
Hàm \(f\left(x\right)\) hiển nhiên liên tục trên R
Do vai trò a;b;c như nhau, không mất tính tổng quát giả sử \(a< b< c\)
\(f\left(a\right)=\left(a-b\right)\left(a-c\right)\)
\(f\left(b\right)=\left(b-a\right)\left(b-c\right)\)
\(f\left(c\right)=\left(c-a\right)\left(c-b\right)\)
\(f\left(a\right).f\left(b\right)=\left(a-b\right)\left(a-c\right)\left(b-a\right)\left(b-c\right)=\left(a-b\right)^2\left(c-a\right)\left(b-c\right)\)
Do \(a< b< c\Rightarrow\left\{{}\begin{matrix}c-a>0\\b-c< 0\end{matrix}\right.\) \(\Rightarrow f\left(a\right).f\left(b\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc (a;b)
\(f\left(b\right).f\left(c\right)=\left(b-a\right)\left(b-c\right)\left(c-a\right)\left(c-b\right)=\left(b-c\right)^2\left(a-b\right)\left(c-a\right)\)
Do \(a< b< c\Rightarrow\left\{{}\begin{matrix}a-b< 0\\c-a>0\end{matrix}\right.\) \(\Rightarrow f\left(b\right).f\left(c\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc (b;c)
Vậy pt đã cho luôn có 2 nghiệm phân biệt
Đúng 0
Bình luận (0)
Cho ba số phức a,b,c phân biệt, khác 0 và thỏa mãn
a
b
c
. Biết một nghiệm của phương trình
a
z
2
+ bz + c 0 có môđun bằng 1. Mệnh đề nào sau đây là đúng? A.
b
2
4ac B.
b
2
ac C.
b
2
2ac D....
Đọc tiếp
Cho ba số phức a,b,c phân biệt, khác 0 và thỏa mãn a = b = c . Biết một nghiệm của phương trình a z 2 + bz + c = 0 có môđun bằng 1. Mệnh đề nào sau đây là đúng?
A. b 2 = 4ac
B. b 2 = ac
C. b 2 = 2ac
D. b 2 = 3ac
Giả sử z 1 ; z 2 là các nghiệm của phương trình a z 2 + bz + c = 0 với z 1 = 1
Theo định lí Viet ta có:
z 1 z 2 = c a ⇔ z 2 = c a 1 z 1 ⇒ z 2 = c a . 1 z 1 = 1
Bởi vì
z 1 + z 2 = - b a a = b ⇒ z 1 + z 2 2 = 1
Suy ra
z 1 + z 2 z 1 + z 2 1 ⇔ z 1 + z 2 1 z 1 + 1 z 2 = 1 ⇔ z 1 + z 2 2 = z 1 z 2 ⇔ b 2 = a c
Đáp án B
Đúng 0
Bình luận (0)
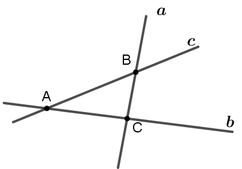
Cho ba đường thẳng a, b, c đôi một cắt nhau và không đồng phẳng. Tìm số giao điểm phân biệt của ba đường thẳng đã cho.
A. 6
B. 2
C. 1
D. 3
Đáp án C
Nếu ba đường thẳng a,b,c đôi một cắt nhau và không đồng phẳng thì chúng chỉ có thể đồng quy tại một điểm.

Đúng 0
Bình luận (0)
Cho \(a,b,c,p,q,r\)đôi một phân biệt. Giải hệ phương trình: \(\hept{\begin{cases}\frac{x}{a-q}+\frac{y}{b-q}+\frac{z}{c-q}=1\\\frac{x}{a-p}+\frac{y}{b-p}+\frac{z}{c-p}=1\\\frac{x}{a-r}+\frac{y}{b-r}+\frac{z}{c-r}=1\end{cases}}\)
Cách này của mình là suy đoán thui nha
Từ HPT trên: \(\frac{x}{a-q}+\frac{y}{b-q}+\frac{z}{c-q}=\frac{x}{a-p}+\frac{y}{b-p}+\frac{z}{c-p}\)
\(\Leftrightarrow\left(p-q\right)\left[\frac{x}{\left(a-p\right)\left(a-q\right)}+\frac{y}{\left(b-p\right)\left(b-q\right)}+\frac{z}{\left(c-q\right)\left(c-p\right)}\right]=0\)
Chia TH:
TH1:p=q
Tương tự p=r thì cũng thu về p=q=r
TH2: nguyên cái trong ngoặc vuông
Tương đương với: \(ax+by+cz=r\left(x+y+z\right)\)
Tương tự: \(\hept{\begin{cases}ax+by+cz=p\left(x+y+z\right)\\ax+by+cz=q\left(x+y+z\right)\end{cases}}\)
Cũng thu đc p=q=r
Do đó từ 2 TH cũng thu về PT:
\(\frac{x}{a-q}+\frac{y}{b-q}+\frac{z}{c-q}=1\)
Rồi vậy không biết làm tiếp :D
À, xin lỗi, mình đánh bị thiếu điều kiện, mình sửa lại rồi đó
Trl :
Bạn kia làm đúng rồi nhé !
Học tốt nhé bạn @
a) Chứng minh rằng với a, b , c là các số thực thì phương trình sau luôn có nghiệm:(x – a)(x – b) + (x – b)(x – c) + (x – c)(x – a) 0b) Chứng minh rằng với ba số thức a, b , c phân biệt thì phương trình sau có hai nghiệm phân biết: c) Chứng minh rằng phương trình: c2x2 + (a2 – b2 – c2)x + b2 0 vô nghiệm với a, b, c là độ dài ba cạnh của một tam giác.d) Chứng minh rằng phương trình bậc hai:(a + b)2x2 – (a – b)(a2 – b2)x – 2ab(a2 + b2) 0 luôn có hai nghiệm phân biệt.
Đọc tiếp
a) Chứng minh rằng với a, b , c là các số thực thì phương trình sau luôn có nghiệm:
(x – a)(x – b) + (x – b)(x – c) + (x – c)(x – a) = 0
b) Chứng minh rằng với ba số thức a, b , c phân biệt thì phương trình sau có hai nghiệm phân biết: 
c) Chứng minh rằng phương trình: c2x2 + (a2 – b2 – c2)x + b2 = 0 vô nghiệm với a, b, c là độ dài ba cạnh của một tam giác.
d) Chứng minh rằng phương trình bậc hai:
(a + b)2x2 – (a – b)(a2 – b2)x – 2ab(a2 + b2) = 0 luôn có hai nghiệm phân biệt.
12345x331=...///???......................ai nhanh mk tk cho
Đúng 0
Bình luận (0)
mk ko biet dang cau hoi nen phai the thoi mong cac ban thon cam
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giải phương trình (x là ẩn số ; a,b,c là hằng số và đôi một khác nhau)
1/(a+b-x) = 1/a +1/b + 1/x
Giúp mình với


