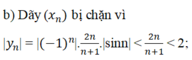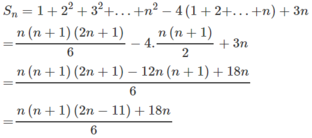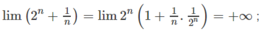Xét tính bị chặn của các dãy số với số hạng tổng quát sau: x n = 5 n 2 n 2 + 3
PB
Những câu hỏi liên quan
Xét tính bị chặn của các dãy số với số hạng tổng quát sau: z n = n cos n π
Xét tính bị chặn của các dãy số với số hạng tổng quát sau: y n = - 1 n 2 n n + 1 sin n
Xét tính bị chặn của các dãy số với số hạng tổng quát sau :
a) \(x_n=\dfrac{5n^2}{n^2+3}\)
b) \(y_n=\left(-1\right)^n\dfrac{2n}{n+1}\sin n\)
c) \(z_n=n\cos n\pi\)
Xét tính tăng, giảm và bị chặn của mỗi dãy số \(\left( {{u_n}} \right)\) sau, biết số hạng tổng quát:
a) \({u_n} = \frac{{{n^2}}}{{n + 1}}\)
b) \({u_n} = \frac{2}{{{5^n}}}\)
c) \({u_n} = {\left( { - 1} \right)^n}.{n^2}\)
a) Ta có: \({u_{n + 1}} = \frac{{{{\left( {n + 1} \right)}^2}}}{{n + 1 + 1}} = \frac{{{{\left( {n + 1} \right)}^2}}}{{n + 2}}\)
Xét hiệu \({u_{n + 1}} - {u_n} = \frac{{{{\left( {n + 1} \right)}^2}}}{{n + 2}} - \frac{{{n^2}}}{{n + 1}} = \frac{{{{\left( {n + 1} \right)}^3} - {n^2}\left( {n + 2} \right)}}{{\left( {n + 2} \right)\left( {n + 1} \right)}} = \frac{{{n^3} + 3{n^2} + 3n + 1 - {n^3} - 2{n^2}}}{{\left( {n + 2} \right)\left( {n + 1} \right)}}\)
\( = \frac{{{n^2} + 3n + 1}}{{\left( {n + 2} \right)\left( {n + 1} \right)}} > 0\) với mọi n ∈ ℕ*.
Vì vậy dãy số đã cho là dãy số tăng.
b) Ta có: \({u_{n + 1}} = \frac{2}{{{5^{n + 1}}}}\)
Xét hiệu \({u_{n + 1}} - {u_n} = \frac{2}{{{5^{n + 1}}}} - \frac{2}{{{5^n}}} = - \frac{4}{5}.\frac{2}{{{5^n}}} = - \frac{8}{{{5^{n + 1}}}} < 0\)
Vì vậy dãy số đã cho là dãy số giảm.
Đúng 0
Bình luận (0)
Xét tính bị chặn của các dãy số sau:
u
n
(
-
1
)
n
A. Bị chặn B. Không bị chặn C. Bị chặn trên D. Bị chặn dưới
Đọc tiếp
Xét tính bị chặn của các dãy số sau: u n = ( - 1 ) n
A. Bị chặn
B. Không bị chặn
C. Bị chặn trên
D. Bị chặn dưới
Cho dãy số
(
u
n
)
với
u
n
n
2
-
4
n
+
3
a) Viết công thức truy hồi của dãy số;b) Chứng minh dãy số bị chặn dưới;c) Tính tổng n số hạng đầu của dãy đã cho.
Đọc tiếp
Cho dãy số ( u n ) với u n = n 2 - 4 n + 3
a) Viết công thức truy hồi của dãy số;
b) Chứng minh dãy số bị chặn dưới;
c) Tính tổng n số hạng đầu của dãy đã cho.
Tính giới hạn của các dãy số có số hạng tổng quát sau đây, khi n → + ∞ u n = 2 n + 1 n
Tính giới hạn của các dãy số có số hạng tổng quát sau đây, khi n → + ∞ v n = - 2 π n + 3 n 4 n
l i m v n = l i m - 2 π n + 3 n 4 n = 0
Đúng 0
Bình luận (0)
6) cho dãy số có các số hạng đầu tiên là 8,15,22,29,36,.. số hạng tổng quát của dãy số là7) cho dãy số left(u_nright) với u_ndfrac{2n+5}{5n-4} với mọi n ϵ N* cho biết số hạng thứ n là dfrac{7}{12}, giá trị của n là8) cho dãy số left(u_nright) với u_ndfrac{2n}{n^2+1} với mọi n ϵ N* số dfrac{9}{41} là số hạng thứ bao nhiêu trong dãy số9) trong các dãy số left(u_nright) cho bởi số hạng tổng quát u_n sau, dãy số nào là dãy số tăngA.u_nleft(dfrac{2}{3}right)^nB. u_ndfrac{n}{n+1}C. u_ndfrac{2}{n.left...
Đọc tiếp
6) cho dãy số có các số hạng đầu tiên là 8,15,22,29,36,.. số hạng tổng quát của dãy số là
7) cho dãy số \(\left(u_n\right)\) với \(u_n=\dfrac{2n+5}{5n-4}\) với mọi n ϵ N* cho biết số hạng thứ n là \(\dfrac{7}{12}\), giá trị của n là
8) cho dãy số \(\left(u_n\right)\) với \(u_n=\dfrac{2n}{n^2+1}\) với mọi n ϵ N* số \(\dfrac{9}{41}\) là số hạng thứ bao nhiêu trong dãy số
9) trong các dãy số \(\left(u_n\right)\) cho bởi số hạng tổng quát \(u_n\) sau, dãy số nào là dãy số tăng
A.\(u_n=\left(\dfrac{2}{3}\right)^n\)
B. \(u_n=\dfrac{n}{n+1}\)
C. \(u_n=\dfrac{2}{n.\left(n+1\right)}\)
D. \(u_n=\dfrac{n+1}{n}\)
10) trong các dãy số \(\left(u_n\right)\) cho bởi số hạng tổng quát \(u_n\) sau, dãy số nào là dãy số giảmA. \(u_n=3^n\)B. \(u_n=\dfrac{n-3}{n+1}\)C. \(u_n=\dfrac{n+4}{n+2}\)D. \(u_n=n^4+2\)6:
\(u_n=8+7\left(n-1\right)=7n+1\)
7: Đặt un=7/12
=>\(\dfrac{2n+5}{5n-4}=\dfrac{7}{12}\)
=>35n-28=24n+60
=>11n=88
=>n=8
=>Đây là số hạng thứ 8
8: \(\dfrac{2n}{n^2+1}=\dfrac{9}{41}\)
=>9n^2+9=82n
=>9n^2-82n+9=0
=>(9n-1)(n-9)=0
=>n=9(nhận) hoặc n=1/9(loại)
=>Đây là số thứ 9
10B
9D
Đúng 0
Bình luận (0)