Tìm giá trị lớn nhất của hàm số f ( x ) = sin ( π | sin x | ) .
A. 1
B. 1 4
C. 1 2
D. 0
Giá trị lớn nhất của hàm số f(x) = sin x + cos 2x trên [0; π ] là
A. 5 4
B. 1
C. 2
D. 9 8
Tìm giá trị lớn nhất và nhỏ nhất của hàm số : Y= 3/ 2+sin(π/3 +x)
\(sin\left(\dfrac{\pi}{3}+x\right)\in\left[-1;1\right]\)
\(\Rightarrow y=\dfrac{3}{2}+sin\left(\dfrac{\pi}{3}+x\right)\in\left[\dfrac{1}{2};\dfrac{5}{2}\right]\)
\(\Rightarrow\left\{{}\begin{matrix}y_{min}=\dfrac{1}{2}\\y_{max}=\dfrac{5}{2}\end{matrix}\right.\)
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
a) \(y=f\left(x\right)=\dfrac{4}{\sqrt{5-2\cos^2x\sin^2x}}\)
b)\(y=f\left(x\right)=3\sin^2x+5\cos^2x-4\cos2x-2\)
c)\(y=f\left(x\right)=\sin^6x+\cos^6x+2\forall x\in\left[\dfrac{-\pi}{2};\dfrac{\pi}{2}\right]\)
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số :
a. y=\(\sqrt{\text{3(1+ sin(x))}}\)-5
b. y= 6 sin(x+8)-5
Tìm giá trị lớn nhất , giá trị hỏ nhất của hàm số:
a) f(x) = sin11x + cos11x
b) f(x) = sin2nx + cos2nx với n\(\in\)N*
Tìm giá trị lớn nhất của hàm số \(y=f\left(x\right)=sin^2x+4sinx-5\) trên \(\left[0;\dfrac{\pi}{2}\right]\)
A. \(-5\)
B. \(5\)
C. \(1\)
D. \(0\)
\(f'\left(x\right)=\left(sin^2x\right)'+4\cdot\left(sinx'\right)-5'\)
\(=2\cdot sinx\cdot cosx+4\cdot cosx=2cosx\left(sinx+2\right)\)
\(f'\left(x\right)=0\)
=>\(cosx\left(sinx+2\right)=0\)
=>\(cosx=0\)
=>\(x=\dfrac{\Omega}{2}+k\Omega\)
mà \(x\in\left[0;\dfrac{\Omega}{2}\right]\)
nên \(x=\dfrac{\Omega}{2}\)
\(f\left(\dfrac{\Omega}{2}\right)=sin^2\left(\dfrac{\Omega}{2}\right)+4\cdot sin\left(\dfrac{\Omega}{2}\right)-5\)
=1+4-5=0
\(f\left(0\right)=sin^20+4\cdot sin0-5=-5\)
=>Chọn D
Cho hàm số y = f(x) có bảng xét dấu biến thiên như sau:
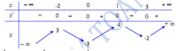
Giá trị lớn nhất của hàm số f(sin x - 1) bằng
A. 3
B. 3
C. -3
D. -2
Chọn B
Đặt ![]()
Bài toán quy về tìm giá trị lớn nhất của hàm số y = f(t) trên đoạn [-2;0].
Từ bảng biến thiên ta có giá trị lớn nhất của hàm số y = f(t) trên đoạn [-2;0] là 3.
Vậy giá trị lớn nhất của hàm số f(sin x -1) bằng 3.
tìm giá trị lớn nhất giá trị nhỏ nhất của hàm số y=căn(1-sin(x²))-1
\(-1\le sin\left(x^2\right)\le1\Rightarrow\)\(0\le\sqrt{1-sin\left(x^2\right)}\le\sqrt{2}\Rightarrow-1\le y\le\sqrt{2}-1\)
\(y_{min}=-1\) khi \(sin\left(x^2\right)=1\Rightarrow x=\pm\sqrt{\dfrac{\pi}{2}+k2\pi}\) (\(k\in N\))
\(y_{max}=\sqrt{2}-1\) khi \(sin\left(x^2\right)=-1\Rightarrow x=\pm\sqrt{-\dfrac{\pi}{2}+k2\pi}\) (\(k\in Z^+\))
Cho hàm số y=\(\dfrac{sin^2x}{cosx\left(sinx-cosx\right)}+\dfrac{1}{4}\) với x thuộc \(\left(\dfrac{\text{π}}{4};\dfrac{\text{π}}{2}\right)\). Tìm giá trị nhỏ nhất của hàm số
y = \(\dfrac{sin^2x}{cosx\left(sinx-cosx\right)}+\dfrac{1}{4}\)
y = \(\dfrac{sin^2x}{sinx.cosx-cos^2x}+\dfrac{1}{4}=\dfrac{\dfrac{sin^2x}{cos^2x}}{\dfrac{sinx.cosx}{cos^2x}-1}+\dfrac{1}{4}\)
y = \(\dfrac{tan^2x}{tanx-1}+\dfrac{1}{4}\)
y = \(\dfrac{4tan^2x+tanx-1}{4tanx-4}\). Đặt t = tanx. Do x ∈ \(\left(\dfrac{\pi}{4};\dfrac{\pi}{2}\right)\) nên t ∈ (1 ; +\(\infty\))\
Ta đươc hàm số f(t) = \(\dfrac{4t^2+t-1}{4t-4}\)
⇒ ymin = \(\dfrac{17}{4}\) khi t = 2. hay x = arctan(2) + kπ