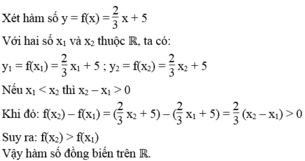cho hàm số y=f(x)=3x-2, chứng minh hàm số luôn đồng biến trên R
TL
Những câu hỏi liên quan
Cho hàm số y=3/7x -8
a)Tính f(0),f(2),f(-1),f(-2)
b)Chứng minh hàm số luôn đồng biến trên R
a) \(f\left(0\right)=\dfrac{2}{7}.0-8=-8\)
\(f\left(2\right)=\dfrac{3}{7}.2-8=-\dfrac{50}{7}\)
\(f\left(-1\right)=\dfrac{3}{7}.\left(-1\right)-8=-\dfrac{59}{7}\)
\(f\left(-2\right)=\dfrac{3}{7}.\left(-2\right)-8=-\dfrac{62}{7}\)
b) Với mọi \(x_1,x_2\in R\), ta có
\(x_1>x_2\Leftrightarrow\dfrac{3}{7}x_1>\dfrac{3}{7}x_2\Leftrightarrow\dfrac{3}{7}x_1-8>\dfrac{3}{7}x_2-8\Leftrightarrow f\left(x_1\right)>f\left(x_2\right)\)
\(\Rightarrow\) Hàm số luôn đồng biến trên R
Đúng 2
Bình luận (0)
b: Vì \(a=\dfrac{3}{7}>0\) nên hàm số đồng biến trên R
Đúng 2
Bình luận (0)
Cho hàm số bậc nhất y=f(x)=(m^2+m+1)x+5.Chứng minh rằng:hàm số luôn đồng biến trên R
`a=m^2+m+1=m^2+2.m. 1/2 + (1/2)^2 + 3/4= (m+1/2)^2 + 3/4 >0 forall m`
`=> a>0 =>` Hàm số luôn đồng biến trên `RR`.
Đúng 2
Bình luận (2)
Để hàm số trên đồng biến khi \(m^2+m+1=m^2+m+\dfrac{1}{4}+\dfrac{3}{4}=\left(m+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\)
Vậy hàm số luôn đồng biến trên R
Đúng 2
Bình luận (1)
Ta có: \(m^2+m+1\)
\(=m^2+2\cdot m\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(m+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\forall m\)
Do đó: Hàm số \(f\left(x\right)=\left(m^2+m+1\right)x+5\) luôn đồng biến trên R
Đúng 1
Bình luận (1)
Cho hàm số y = f(x) = (3m2 - 7m + 5)x - 2011 (*). Chứng minh hàm số (*) luôn đồng biến trên R với mọi m.
Gia su \(x_1< x_2\)
\(\Rightarrow x_1-x_2< 0\left(1\right)\)
Ta co:
\(f\left(x_1\right)-f\left(x_2\right)=\left(3m^2-7m+5\right)x_1-2011-\left(3m^2-7m+5\right)x_2+2011=\left(x_1-x_2\right)\left(3m^2-7m+5\right)\)Vi la chung minh dong bien nen xet
\(3m^2-7m+5>0\)
Dat \(g\left(m\right)=3m^2-7m+5\)
Ta lai co:
\(\Delta=\left(-7\right)^2-4.3.5=-11< 0\)
Theo dinh li dau tam thuc bac hai thi \(g\left(m\right)\)cung dau voi he so 3
\(\Rightarrow3m^2-7m+5>0\left(2\right)\left(\forall m\right)\)
Tu \(\left(1\right)\)va \(\left(2\right)\)suy ra;
\(\left(x_1-x_2\right)\left(3m^2-7m+5\right)< 0\)
Ma \(f\left(x_1\right)-f\left(x_2\right)=\left(x_1-x_2\right)\left(3m^2-7m+5\right)\)
\(\Rightarrow f\left(x_1\right)< f\left(x_2\right)\)
Vay ham so \(y=f\left(x\right)=\left(3m^2-7m+5\right)x-2011\)dong bien voi moi m
Đúng 0
Bình luận (0)
Cho hàm số y = f(x) = 2 3 x + 5 với x ∈ R. Chứng minh rằng hàm số đồng biến trên R.
Cho hàm số y f(x) 3x.Cho x hai giá trị bất kì
x
1
,
x
2
sao cho
x
1
x
2
Hãy chứng minh
f
(
x
1
)
f
(
x
2
)
rồi rút ra kết luận hàm số đã cho đồng biến trên R.
Đọc tiếp
Cho hàm số y = f(x) = 3x.
Cho x hai giá trị bất kì x 1 , x 2 sao cho x 1 < x 2
Hãy chứng minh f ( x 1 ) < f ( x 2 ) rồi rút ra kết luận hàm số đã cho đồng biến trên R.
Cho x các giá trị bất kì x 1 , x 2 sao cho x 1 < x 2
= > x 1 - x 2 < 0
Ta có:
f x 1 = 3 x 1 ; f x 2 = 3 x 2 ⇒ f x 1 − f x 2 = 3 x 1 − 3 x 2 = 3 x 1 − x 2 < 0 ⇒ f x 1 < f x 2
Vậy với x 1 < x 2 ta được f ( x 1 ) < f ( x 2 ) nên hàm số y = 3x đồng biến trên tập hợp số thực R.
Đúng 0
Bình luận (0)
Cho hàm số y = f(x) = 3x.
Cho x hai giá trị bất kì x1, x2 sao cho x1 < x2.
Hãy chứng minh f(x1) < f(x2) rồi rút ra kết luận hàm số đã cho đồng biến trên R.
Cho x các giá trị bất kì x1, x2 sao cho x1 < x2
=> x1 - x2 < 0
Ta có: f(x1) = 3x1 ; f( x2) = 3x2
=> f(x1) - f(x2) = 3x1 - 3x2 = 3(x1 - x2) < 0
=> f(x1) < f(x2)
Vậy với x1 < x2 ta được f(x1) < f(x2) nên hàm số y = 3x đồng biến trên tập hợp số thực R.
Đúng 0
Bình luận (0)
Cho hàm số bậc nhất y f(x) 3x + 1.Cho x hai giá trị bất kì
x
1
,
x
2
, sao cho
x
1
x
2
. Hãy chứng minh
f
(
x
1
)
f
(
x
2
)
rồi rút ra kết...
Đọc tiếp
Cho hàm số bậc nhất y = f(x) = 3x + 1.
Cho x hai giá trị bất kì x 1 , x 2 , sao cho x 1 < x 2 . Hãy chứng minh f ( x 1 ) < f ( x 2 ) rồi rút ra kết luận hàm số đồng biến trên R.
Do x 1 < x 2 nên x 1 − x 2 < 0
Ta có:
f x 1 − f x 2 = 3 x 1 + 1 − 3 x 2 + 1 = 3 x 1 − x 2 < 0 ⇔ f x 1 < f x 2
Vậy hàm số y = 3x + 1 đồng biến trên R
Đúng 0
Bình luận (0)
Cho hàm số bậc nhất y = f(x) = 3x + 1.
Cho x hai giá trị bất kì x1, x2, sao cho x1 < x2. Hãy chứng minh f(x1) < f(x2) rồi rút ra kết luận hàm số đồng biến trên R.
Do x1 < x2 nên x1 - x2 < 0
Ta có: f(x1 ) - f(x2 )=(3x1 + 1) - (3x2 + 1) = 3(x1 - x2 ) < 0
⇔ f(x1 ) < f(x2 )
Vậy hàm số y = 3x + 1 đồng biến trên R
Đúng 0
Bình luận (0)
Cho hàm số y=-5/9x-6
a) Tính f(-1),f(0),f(2),f(1/2)
b)Chứng minh hàm số luôn nghịch biến trên R
b: Vì \(a=-\dfrac{5}{9}< 0\) nên hàm số luôn nghịch biến trên R
Đúng 1
Bình luận (0)