Cho hai đường thẳng d1: 2x + 2 3 y + 5 = 0 và d2: y - 6 = 0. Góc giữa d1 và d2 có số đo bằng:
A. 30 °
B. 45 °
C. 60 °
D. 135 °
PB
Những câu hỏi liên quan
Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng
d
1
:
2
x
-
4
y
-
3
0
và
d
2
:
3
x
-
y
+
17
0
. Số đo góc giữa
d
1
và
d
2
là A.
45...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng d 1 : 2 x - 4 y - 3 = 0 và d 2 : 3 x - y + 17 = 0 . Số đo góc giữa d 1 và d 2 là
A. 45 °
B. 90 °
C. 30 °
D. 60 °
cho 2 đường thẳng d1: x + 2y + 4 = 0; d2: 2x - y + 6 = 0. Số đo góc giữa d1; d2 là:
A. 300
B. 600
C. 450
D. 900
\(d_1\) nhận \(\overrightarrow{n_1}=\left(1;2\right)\) là 1 vtpt
\(d_2\) nhận \(\overrightarrow{n_2}=\left(2;-1\right)\) là 1 vtpt
Do \(\overrightarrow{n_1}.\overrightarrow{n_2}=1.2+2.\left(-1\right)=0\Rightarrow d_1\perp d_2\)
hay góc giữa 2 đường thẳng là 90 độ
Đúng 0
Bình luận (0)
Cho d1:2x+5y+4=0 và d2:5x-2y+6=0.Số đo của góc giữa 2 đường thẳng d1 và d2 là? A.90° B.60° C.45° D.30°
Xem thêm câu trả lời
Tìm số đo của góc giữa hai đường thẳng d1 và d2 lần lượt có phương trình: d1: 4x – 2y + 6 = 0 và d2: x – 3y + 1 = 0
Với d1: 4x – 2y + 6 = 0 có vecto pháp tuyến là: n1→(4;-2)
và d2: x – 3y + 1 = 0 có vecto pháp tuyến là: n2→(1;-3) ; ta có :
Đúng 2
Bình luận (0)
Cho điểm A(1; 3) và hai đường thẳng
d
1
:
2
x
−
3
y
+
4
0
,
d
2
:
3
x
+
y
0
. Số đường thẳng qua A và tạo với
d
1
,
d
2
các góc bằng nhau là A.1 B.2 C.4 D.Vô số
Đọc tiếp
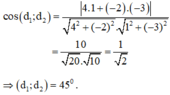
Cho điểm A(1; 3) và hai đường thẳng d 1 : 2 x − 3 y + 4 = 0 , d 2 : 3 x + y = 0 . Số đường thẳng qua A và tạo với d 1 , d 2 các góc bằng nhau là
A.1
B.2
C.4
D.Vô số
ĐÁP ÁN B
Đường thẳng qua A và tạo với d1d2 các góc bằng nhau khi vuông góc với phân giác của góc tạo bởi d1d2.
Do vậy số lượng đường thẳng cần tìm là 2.
Đúng 0
Bình luận (0)
Góc giữa hai đường thẳng d1: 3x + y - 3 = 0 và d2: 2x - y + 2 = 0 bằng bao nhiêu?
A. 30 °
B. 45 °
C. 60 °
D. 90 °
Đáp án: B
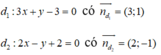
Gọi góc giữa hai đường thẳng là α
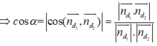
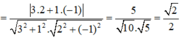
⇒ α = 45 °
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho hai đường thẳng
d
1
:
x
−
3
−
1
y
−
3
−...
Đọc tiếp
Trong không gian Oxyz, cho hai đường thẳng d 1 : x − 3 − 1 = y − 3 − 2 = z + 2 1 ; d 2 : x − 5 − 3 = y + 1 2 = z − 2 1 và P : x + 2 y + 3 z − 5 = 0. Đường thẳng vuông góc với (P) và cắt d 1 , d 2 có phương trình là:
A. x − 1 1 = y + 1 2 = z 3 .
B. x − 2 1 = y − 3 2 = z − 1 3 .
C. x − 3 1 = y − 3 2 = z + 2 3 .
D. x − 1 3 = y + 1 2 = z 1 .
3) cho hai đường thẳng : y=x-(d1) ;y=-x+3(d2 A) vẽ đồ thị hàm số (d1);(d2) . Viết phương trình đường thẳng đi qua A và 0 (0 là góc tọa độ) B ) tính góc anpha tao bởi (d1) và trục hoành ox
Trong không gian Oxyz, cho hai đường thẳng
d
1
:
x
-
3
1
y
-
3
-
2
z
+
2
1
,
d
2
:...
Đọc tiếp
Trong không gian Oxyz, cho hai đường thẳng d 1 : x - 3 1 = y - 3 - 2 = z + 2 1 , d 2 : x - 5 - 3 = y + 1 2 = z - 2 1 và (P): x+2y+3z-5=0. Đường thẳng vuông góc với (P) và cắt d 1 , d 2 có phương trình là:
A. x - 1 1 = y + 1 2 = z 3
B. x - 2 1 = y - 3 2 = z - 1 3
C. x - 3 1 = y - 3 2 = z + 2 3
D. x - 1 3 = y + 1 2 = z 1
