Biết x1, x2 là hai nghiệm của phương trình log 7 4 x 2 - 4 x + 1 2 x + 4 x 2 + 1 = 6 x và x1, x2 thỏa mãn x 1 + 2 x 2 = 1 4 a + b với a, b là hai số nguyên dương. Tính a + b.
A. a + b = 16
B. a + b = 11
C. a + b = 14
D. a + b = 13
Gọi x 1 , x 2 là hai nghiệm của phương trình log 2 x + log 3 x . log 27 - 4 = 0 .Giá trị của biểu thức log x 1 + log x 2 bằng
A. 3
B. -3
C. -4
D. 4
Cho phương trình : x2+(m-1)x-m2-2=0 (m là tham số).Tìm giá trị của m để phương trình có hai nghiệm trái dấu thỏa mãn 2|x1|-|x2|=4(biết x1<x1)
Ta có: \(x^2-2\left(m+1\right)x+m-4=0\)
Phương trình có hai nghiệm phân biệt khi △'>0\(\Leftrightarrow\left(m+1\right)^2-m+4>0\Leftrightarrow m^2+m+5>0\)(luôn đúng)
Theo Vi-ét \(x_1+x_2=2\left(m+1\right);x_1x_2=m-4\)
\(A=x_1+x_2-2x_1x_2+2021=2\left(m+1\right)-2\left(m-4\right)+2021=2031\) không phụ thuộc vào m
Cho phương trình x2+ 2(m − 1)x − 6m − 7 = 0 (1) (m là tham số).
a) Chứng minh rằng với mọi giá trị của m thì phương trình (1) luôn có hai nghiệm phân biệt.
b) Gọi x1, x2là hai nghiệm của phương trình (1). Tìm các giá trị của m thỏa x1(x1+3/3x2)+x2(x2+3/2x1)=15
các bạn ai biết thì chỉ giúp mình với ạ
\(x^{2^{ }}+2\left(m-1\right)x-6m-7=0\left(1\right)\)
a) \(Dental=\left[2\left(m-1\right)\right]^2-4\cdot1\cdot\left(-6m-7\right)\)
\(< =>4\cdot\left(m^2-2m+1\right)+24m+28\)
\(< =>4m^2-8m+4+24m+28\)
\(< =>4m^2+16m+32\)
\(< =>\left(2m+4\right)^2+16>0\) với mọi m
Vậy phương (1) luôn có 2 nghiệm phân biệt với mọi m
b) Theo định lí vi ét ta có:
x1+x2= \(\dfrac{-2\left(m-1\right)}{1}=-2m+1\)
x1x2= \(-6m-7\)
quy đồng
khử mẫu
tách sao cho có tích và tổng
thay x1x2 x1+x2
kết luận
mặt xấu vl . . .![]()
Cho x1, x2 là hai nghiệm của phương trình: x^2-2x-1=0.Hãy lập một phương trình bậc hai một ẩn có hại nghiệm là x1+(x2)^2 và x2+(x1)^2
\(x^2-2x-1=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=-1\end{matrix}\right.\)
Đặt \(\left\{{}\begin{matrix}u=x_1+\left(x_2\right)^2\\v=x_2+\left(x_1\right)^2\end{matrix}\right.\)
\(\Rightarrow\)\(\left\{{}\begin{matrix}u+v=\left(x_1+x_2\right)+\left(x_2+x_1\right)^2-2x_1x_2\\uv=2x_1x_2+x_1^3+x_2^3=2x_1x_2+\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u+v=8\\uv=12\end{matrix}\right.\)
=>u và v là nghiệm của pt \(t^2-8t+12=0\)
Biết rằng phương trình x - 2 log 2 4 x - 2 = 4 . x - 2 3 có hai nghiệm x1, x2 (x1 < x2). Tính 2x1 – x2.
A. 1.
B. 3.
C. -5.
D. -1.
Đáp án D.
ĐK: x > 2.
TH1: Ta thấy x = 3 không phải là nghiệm của PT.
TH2: Với x ≠ 3 logarit cơ số x – 2 cả 2 vế ta được
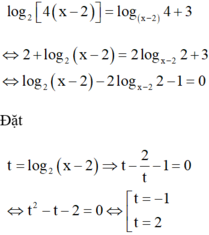
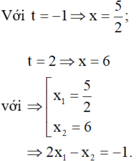
Giả sử x1, x2 là hai nghiệm của phương trình: x2 – x + A = 0 và x3, x4 là hai nghiệm của phương trình: x2 – 4x + B = 0. Tính A, B biết rằng x1, x2, x3, x4 lập thành một cấp số nhân tăng?
Biết phương trình 2log3(x – 2) + log3( x – 4)2 = 0 có hai nghiệm x1, x2. Khi đó (x1 – x2)2 bằng:
A. 2
B. 8
C. 9
D. 4
Chọn A.
ĐK: x > 2
Pt ⇔ log3(x – 2)2(x – 4)2 = 0
⇔ (x – 2)2(x – 4)2 = 1
Với 2 < x< 4 suy ra (x - 2)(4 - x) = 1 ⇔ x = 3 (tm)
Với x ≥ 4 suy ra (x - 2)(x - 4) = 1 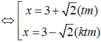
Suy ra (x1 – x2)2 = (3 – 3 – √2)2 = 2
Cho phương trình: x^2 -6x +m+1=0(1)( với m là tham số )
a, giải phương trình (1) khi m=4
b, Gọi hai nghiệm của phương trình (1) là x1 ;x2. Tìm giá trị của m để x1; x2 thỏa mãn x1^2 +x2^2=3(x1+ x2)
Làm câu b)
Để phương trình có hai nghiệm phân biệt:
\(\Delta'\ge0\Leftrightarrow3^2-\left(m+1\right)\ge0\Leftrightarrow m\le8\)
Áp dụng định lí Vi-ét ta có:
\(\hept{\begin{cases}x_1+x_2=6\\x_1.x_2=m+1\end{cases}}\)(1)
Xét: \(x^2_1+x^2_2=3\left(x_1+x_2\right)\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=3\left(x_1+x_2\right)\)(2)
Từ 1, 2 ta có:
\(6^2-2\left(m+1\right)=3.6\Leftrightarrow m=8\)(tm)
Vậy ...
PT $(*)$ là PT bậc nhất ẩn $x$ thì làm sao mà có $x_1,x_2$ được hả bạn?
PT cuối cũng bị lỗi.
Bạn xem lại đề!
Lời giải:
a)
Ta có: $\Delta'=m^2-(2m-2)=m^2-2m+2=(m-1)^2+1>0$ với mọi $m\in\mathbb{R}$
Do đó pt luôn có 2 nghiệm phân biệt $x_1,x_2$ với mọi $m\in\mathbb{R}$
b)
Áp dụng định lý Viet: \(\left\{\begin{matrix} x_1+x_2=-2m\\ x_1x_2=2m-2\end{matrix}\right.\)
Để $x_1^2+x_2^2-3x_1x_2=4$
$\Leftrightarrow (x_1+x_2)^2-5x_1x_2=4$
$\Leftrightarrow (-2m)^2-5(2m-2)=4$
$\Leftrightarrow 4m^2-10m+6=0$
$\Leftrightarrow 2m^2-5m+3=0$
$\Leftrightarrow (m-1)(2m-3)=0$
$\Rightarrow m=1$ hoặc $m=\frac{3}{2}$ (đều thỏa mãn)