Tìm tất cả các giá trị thực của tham số m để hàm số chỉ có cực tiểu mà không có cực đại A. B. C. D.
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số 
chỉ có cực tiểu mà không có cực đại
A.
B. 
C.
D.
PB
Những câu hỏi liên quan
Tìm tất cả các giá trị thực của tham số m để hàm số
y
(
m
+
1
)
x
4
-
m
x
2
+
3
2
chỉ có cực tiểu mà không có cực đại A. ...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = ( m + 1 ) x 4 - m x 2 + 3 2 chỉ có cực tiểu mà không có cực đại
A. m < - 1
B. - 1 ≤ m ≤ 0
C. m > 1
D. - 1 ≤ m < 0
Cho hàm số
y
(
m
-
1
)
x
4
-
3
m
x
2
+
5
. Tìm tất cả các giá trị của tham số thực m để hàm số có cực đại mà không có cực tiểu A....
Đọc tiếp
Cho hàm số y = ( m - 1 ) x 4 - 3 m x 2 + 5 . Tìm tất cả các giá trị của tham số thực m để hàm số có cực đại mà không có cực tiểu
A. m ∈ ( - ∞ ; 0 ] ∪ [ 1 ; + ∞ ) .
B. m ∈ 0 ; 1 .
C. m ∈ ( 0 ; 1 ) .
D. m ∈ ( - ∞ ; 0 ) ∪ ( 1 ; + ∞ ) .
Chọn B
[Phương pháp tự luận]
y ' = 4 ( m - 1 ) x 3 - 6 m x = 0 (*)
TH1 : Nếu m = 1 , (*) trở thành : y ' = - 6 x = 0 hay x= 0 , y ' ' = - 6 < 0
Vậy m = 1 hàm số đạt cực đại tại x = 0
TH2 : Nếu m ≠ 1
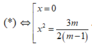
Hàm số có cực đại mà ko có cực tiểu
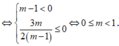
Kết hợp 2 trường hợp : m ∈ [ 0 ; 1 ]
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của tham số m để hàm số y
3
2
x
4
-
2
m
x
2
+
7
3
có cực tiểu mà không có cực đại A. m
≥
0 B. m
≤
0 C. m
≥
1 D. m -1
Đọc tiếp
Tìm tất cả các giá trị của tham số m để hàm số y = 3 2 x 4 - 2 m x 2 + 7 3 có cực tiểu mà không có cực đại
A. m ≥ 0
B. m ≤ 0
C. m ≥ 1
D. m = -1
Chọn B.
Hàm số trùng phương 
có một cực tiểu mà không có cực đại khi
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của tham số m để hàm số
y
3
2
x
4
-
2
m
x
2
+
7
3
có cực tiểu mà không có cực đại A.
m...
Đọc tiếp
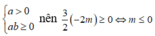
Tìm tất cả các giá trị của tham số m để hàm số y = 3 2 x 4 - 2 m x 2 + 7 3 có cực tiểu mà không có cực đại
A. m ≥ 0 .
B. m ≤ 0 .
C. m ≥ 1 .
D.m=-1
Tìm tất cả giá trị của tham số m để hàm số y = 1 2 x 4 – m x 2 + 3 2 có cực tiểu mà không có cực đại
A. m ≤ 0
B. m = -1
C. m ≥ 1
D. m ≥ 0
Chọn A.
Ta có y ' = 2 x 3 - 2 m x = 2 x x 2 - m
m > 0 thì y’=0 có ba nghiệm phân biệt và hàm số có một cực tiểu, hai cực đại.
m ≤ 0 thì y’ = 0 có nghiệm duy nhất x = 0 là điểm cực tiểu của hàm số.
Vậy m ≤ 0
Đúng 0
Bình luận (0)
Để đồ thị hàm số
y
-
x
4
-
(
m
-
3
)
x
+
2
m
+
1
có điểm cực đại mà không có điểm cực tiểu thì tất cả các giá trị thực của tham số m là A.
m
≤
3
B. m 3 C.
m
≥
3
D. m 3
Đọc tiếp
Để đồ thị hàm số y = - x 4 - ( m - 3 ) x + 2 m + 1 có điểm cực đại mà không có điểm cực tiểu thì tất cả các giá trị thực của tham số m là
A. m ≤ 3
B. m < 3
C. m ≥ 3
D. m > 3
Tìm tất cả các giá trị thực của tham số m để hàm số
y
mx
4
+
(
m
-
1
)
x
2
+
2
có đúng 1 điểm cực đại và không có điểm cực tiểu. A. . B. . C. . D. .
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = mx 4 + ( m - 1 ) x 2 + 2 có đúng 1 điểm cực đại và không có điểm cực tiểu.
A. 
.
B.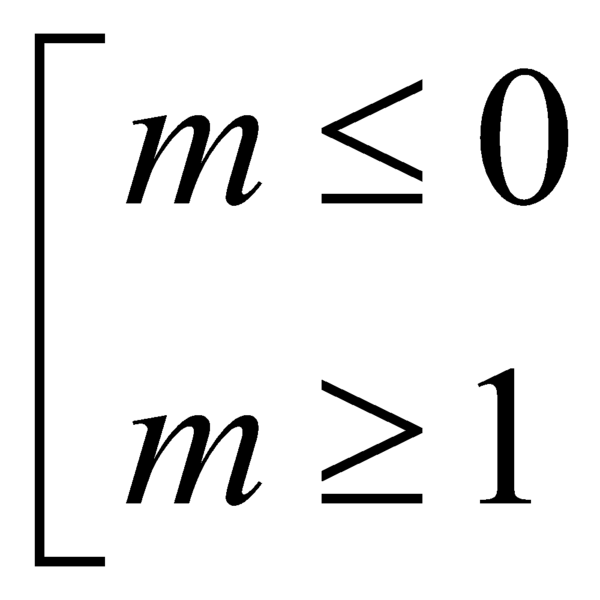 
.
C. 
.
D. 
.
Đáp án C
TH1: 
suy ra 
hàm số có 
điểm cực đại 
nhận m=0.
TH2: 
.
Theo yêu cầu bài toán
.
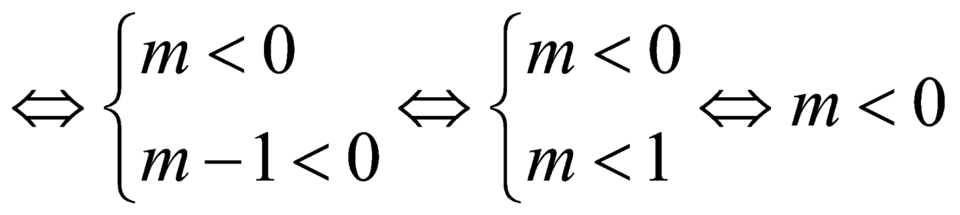Vậy 
là giá trị cần tìm.
Đúng 0
Bình luận (0)
H24
22 tháng 8 2021 lúc 20:34
Câu 3 Để đồ thị hàm số \(y=-x^4-\left(m-3\right)x^2+m+1\) có điểm cực đạt mà không có điểm cực tiểu thì tất cả giá trị thực của tham số m là
Câu 4 Cho hàm số \(y=x^4-2mx^2+m\) .Tìm tất cả các giá trị thực của m để hàm số có 3 cực trị
Tìm tất cả các giá trị của tham số \(m\) để hàm số \(y=x^4+4mx^3+3\left(m+1\right)x^2+1\) có cực tiểu mà không có cực đại
\(y'=4x^3+12mx^2+6\left(m+1\right)x=2x\left[2x^2+6mx+3\left(m+1\right)\right]\)
Hàm có cực tiểu mà ko có cực đại khi và chỉ khi \(y'=0\) có đúng 1 nghiệm đơn
TH1: \(2x^2+6mx+3\left(m+1\right)=0\) có nghiệm \(x=0\)
\(\Leftrightarrow m=-1\)
TH2: \(2x^2+6mx+3\left(m+1\right)=0\) có ít hơn 2 nghiệm
\(\Leftrightarrow\Delta'=9m^2-6\left(m+1\right)\le0\)
\(\Leftrightarrow\dfrac{1-\sqrt{7}}{3}\le m\le\dfrac{1+\sqrt{7}}{3}\)
Đúng 3
Bình luận (0)