Tìm mệnh đề sai trong các mệnh đề sau:
A. ∫ 2 e x d x = 2 ( e x + C )
B. ∫ x 3 d x = x 4 + C 4
C. ∫ 1 x d x = ln x + C
D. ∫ sin x d x = - cos x + C
Xem xét các mệnh đề sau đúng hay sai và lập mệnh đề phủ định của mỗi mệnh đề:
a) \(\exists x\in Q\), \(4x^2-1=0\)
b) \(\exists n\in N\), \(n^2+1\) chia hết cho 4
c) \(\exists x\in R\), \(\left(x-1\right)^2\ne x-1\)
d) \(\forall n\in N\), \(n^2>n\)
e) \(\exists n\in N\), n(n+!) là một số chính phương
Bài 4. Trong các mệnh đề sau, mệnh đề nào là đúng ? Giải thích ? Phát biểu các mệnh đề đó thành lời: a) x R x2 , 0. b) x R x x2 , c) x Q 2 ,4x 1 0 . d) n N n n 2 , . e) f) x R x x2 x R x x ,5 3 1 2 , 1 0
Cho hai tập hợp E = {x ∈ R: f(x) = 0}; F = {x ∈ R: g(x) = 0}; H = { x ∈ R: f(x)2 + g(x)2 = 0}. Trong các mệnh đề sau, mệnh đề đúng là
A. H = E ∪ F.
B. H = E ∩ F.
C. H = E \ F.
D. H = F \ E.
Đáp án: B
f(x)2 + g(x)2 = 0 ⇔ f(x) = 0 và g(x) = 0. Nghĩa là H là tập hợp bao gồm các phần tử vừa thuộc E vừa thuộc F hay H = E ∩ F
cho mệnh đề chứa biến ''x2 - 3x +2 >0'' Hãy xác định tính đúng sai của các mệnh đề có được khi cho biến x nhận các giá trị sau đây a) x= 2 b) x= 0 c) x= 0,5 d) x= -1
Cho đồ thị (C) của hàm số y' = ( 1 + x ) x + 2 2 x - 3 3 ( 1 - x 2 ) . Trong các mệnh đề sau, tìm mệnh đề sai:
A. (C) có một điểm cực trị.
B. (C) có ba điểm cực trị.
C. (C) có hai điểm cực trị.
D. (C) có bốn điểm cực trị.
Chọn C.
Ta có y' = ( 1 + x ) x + 2 2 x - 3 3 ( 1 - x 2 ) nên y' = 0
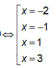
Bảng xét dấu
![]()
Ta thấy đạo hàm đổi dấu 2 lần nên hàm số có hai điểm cực trị suy ra đồ thị hàm số có 2 điểm cực trị.
Trắc nghiệm: Ta thấy phương trình y' = 0 có 2 nghiệm đơn hoặc bội lẻ nên đồ thị hàm số có hai điểm cực trị.
Cho a,b,c là các số thực dương, a ≠ 1 . Xét các mệnh đề sau
I 3 a = 2 ⇔ a = log 3 2 I I ∀ x ∈ ℝ \ 0 , log 2 x 2 = 2 log 2 x I I I log a b c = log a b . log a c
Trong ba mệnh đề I , I I , I I I số mệnh đề sai là
A. 2
B. 3
C. 1
D. 0
Cho a,b,c là các số thực dương, a ≠ 1 . Xét các mệnh đề sau
( I ) 3 a = 2 ⇔ a = log 3 2
( II ) ∀ x ∈ R \ { 0 } , log 2 x 2 = 2 log 2 x
( III ) log a ( bc ) = log a b . log a c
Trong ba mệnh đề (I), (II), (III) số mệnh đề sai là
A. 2
B. 3
C. 1
D. 0
Cho hàm số y = f(x) có đồ thị như hình bên. Tìm mệnh đề sai trong các mệnh đề sau.
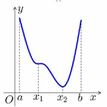
A. Hàm số nghịch biến trong khoảng x 1 ; x 2
B. f ; x > 0 , ∀ x ∈ x 2 ; b
C. Hàm số nghịch biến trong khoảng a ; x 2
D. f ' x < 0 , ∀ x ∈ a ; x 2
Cho hai tập hợp E = {x ∈ R: f(x) = 0}; F = { x ∈ R: g(x) = 0}; H = {x ∈ R: f ( x ) g ( x ) = 0}. Trong các mệnh đề sau, mệnh đề đúng là:
A. H = E ∪ F.
B. H = E ∩ F.
C. H = E \ F.
D. H = F \ E.
Đáp án: C
f(x)/g(x) = 0 ⇔ f(x) = 0 và g(x) ≠ 0. Nghĩa là H là tập hợp bao gồm các phần tử thuộc E nhưng không thuộc F hay H = E \ F.
Cho hai tập hợp E = {x ∈ R: f(x) = 0}; F = { x ∈ R: g(x) = 0}; H = {x ∈ R : f(x).g(x) = 0}. Trong các mệnh đề sau, mệnh đề đúng là:
A. H = E ∪ F.
B. H = E ∩ F.
C. H = E \ F.
D. H = F \ E.
Đáp án: A
f(x).g(x) = 0 ⇔ f(x) = 0 hoặc g(x) = 0. Nghĩa là H là tập hợp bao gồm các phần tử thuộc E hoặc thuộc F hay H = E ∪ F.