Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác ABC. chứng minh rằng D A → + D B → + D C → = 3 D G →
PB
Những câu hỏi liên quan
cho hình tứ diện ABCD. Gọi M là điểm trên cạnh AD sao cho MA = 2MD
a, G là trọng tâm tam giác ABD. Chứng minh rằng: MG // (BCD)
b, H là trọng tâm tam giác ABC. Chứng minh rằng: HG // (BCD)
a: Gọi giao điểm của AG với BC là E
Xét ΔABD có
G là trọng tâm
E là giao điểm của AG với BD
Do đó: E là trung điểm của BD và AG=2/3AE
Xét ΔAHD có \(\dfrac{AG}{AE}=\dfrac{AM}{AD}=\dfrac{2}{3}\)
nên GM//ED
=>GM//BD
mà BD\(\subset\left(BCD\right)\) và GM không thuộc mp(BCD)
nên GM//(BCD)
b: Gọi giao của AH với BC là F
Xét ΔABC có
H là trọng tâm
F là giao điểm của AH với BC
Do đó: F là trung điểm của BC và AH=2/3AF
Xét ΔAGE có \(\dfrac{AH}{AF}=\dfrac{AG}{AE}=\dfrac{2}{3}\)
nên HG//FE
mà \(FE\subset\left(BCD\right)\);HG không thuộc(BCD)
nên HG//(BCD)
Đúng 1
Bình luận (1)
Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác ABC. Chứng minh rằng:
G
D
→
.
G
A
→
+
G
D
→
.
G
B
→
+
G
D...
Đọc tiếp
Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác ABC. Chứng minh rằng: G D → . G A → + G D → . G B → + G D → . G C → = 0
Ta có:
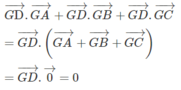
(Vì G là trọng tâm của tam giác ABCD nên 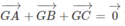 )
)
Đúng 0
Bình luận (0)
1. Cho tứ giác ABCD ( AD không song song BC) có E,F lần lượt là trung điểm AD, BC và EFAB+CD/2. Chứng minh rằng tứ giác ABCD là hình thang.2. Cho tứ giác ABCD có ADBC. Đường thẳng đi qua trung điểm M và N của 2 cạnh AB và CD cắt AD và BC lần lượt tại E và F. Chứng minh góc AEMgóc MFB.3. Cho tam giác ABC (ABAC). Trên cạnh AB lấy điểm D sao cho BDAC. Gọi M,N lần lượt là trung điểm của AD, BC. Chứng minh góc BAC 2.BMN4. Cho tứ giác ABCD, gọi A, B, C, D lần lượt là trọng tâm của các tam giác BCD,...
Đọc tiếp
1. Cho tứ giác ABCD ( AD không song song BC) có E,F lần lượt là trung điểm AD, BC và EF=AB+CD/2. Chứng minh rằng tứ giác ABCD là hình thang.
2. Cho tứ giác ABCD có AD=BC. Đường thẳng đi qua trung điểm M và N của 2 cạnh AB và CD cắt AD và BC lần lượt tại E và F. Chứng minh góc AEM=góc MFB.
3. Cho tam giác ABC (AB>AC). Trên cạnh AB lấy điểm D sao cho BD=AC. Gọi M,N lần lượt là trung điểm của AD, BC. Chứng minh góc BAC = 2.BMN
4. Cho tứ giác ABCD, gọi A', B', C', D' lần lượt là trọng tâm của các tam giác BCD, ACD, ABD, ABC. Chứng minh rằng các đường thẳng AA', BB', CC', DD' đồng quy.
5. Cho tam giác ABC, G là trọng tâm. Đường thẳng d không cắt các cạnh của tam giác ABC. Gọi A', B', C', G' lần lượt là hình chiếu của A, B, C, G trên đường thẳng d. Chứng minh GG'=AA'+BB'+CC'/3
Cho tứ diện ABCD có \(\widehat {CBD} = {90^0}.\)
a) Gọi M, N tương ứng là trung điểm của AB, AD. Chứng minh rằng MN vuông góc
BC.
b) Gọi G, K tương ứng là trọng tâm của các tam giác ABC, ACD. Chứng minh rằng
GK vuông góc với BC.
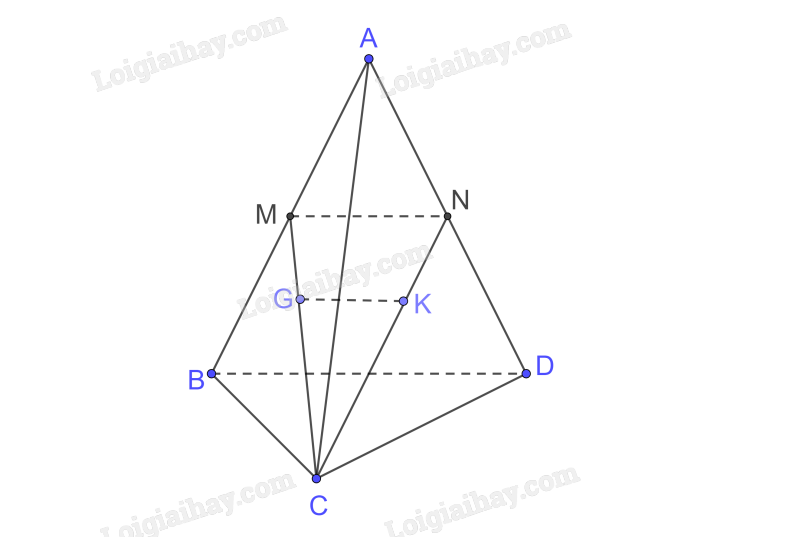
a) Xét tam giác ABD có
M, N tương ứng là trung điểm của AB, AD
\( \Rightarrow \) MN là đường trung bình của tam giác ABD
\( \Rightarrow \) MN // BD mà BD \( \bot \) BC (\(\widehat {CBD} = {90^0}\))
\( \Rightarrow \) MN \( \bot \) BC.
b) Vì G, K tương ứng là trọng tâm của các tam giác ABC, ACD nên \(\frac{{CG}}{{CM}} = \frac{{CK}}{{CN}} = \frac{2}{3}\)
\( \Rightarrow \) GK // MN (Định lý Talet) mà MN \( \bot \) BC
\( \Rightarrow \) GK \( \bot \) BC.
Đúng 0
Bình luận (0)
Cho tứ diện ABCD. Gọi
G
1
,
G
2
,
G
3
lần lượt là trọng tâm các tam giác ABC, ACD, ABD. Chứng minh rằng
(
G
1
G
2
G
3
)
/
/
(
B
C
D
)
.
Đọc tiếp
Cho tứ diện ABCD. Gọi G 1 , G 2 , G 3 lần lượt là trọng tâm các tam giác ABC, ACD, ABD. Chứng minh rằng ( G 1 G 2 G 3 ) / / ( B C D ) .
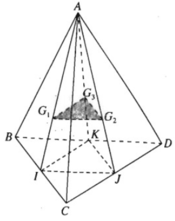
Gọi I, J và K lần lượt là trung điểm của các cạnh BC, CD và BD. Theo tính chất trọng tâm của tam giác ta có:
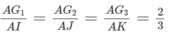
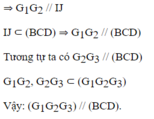
Đúng 0
Bình luận (0)
ho tam giác nhọn ABC có trực tâm H, O là giao điểm các trung trực của tam giác ABC. D là điểm sao cho O là trung điểm AD.
a) Chứng minh rằng tứ giác BHCD là hình bình hành.
b) Gọi M là trung điểm của BC. Chứng minh rằng AH=2OM.
c) Gọi G là trọng tâm của tam giác ABC. CMR: H,G,O thẳng hàng và OG=1/3OH
Trong tứ giác ABCD gọi A', B', C', D' thứ tự là trọng tâm của các tam giác BCD, ACD, ABD, ABC. Chứng minh rằng bốn đường thẳng Â', BB',CC', DD' đồng quy.
I don't now
sorry
.....................
Đúng 0
Bình luận (0)
bn tham khảo ở đây nhé :
https://olm.vn/hoi-dap/question/1016726.html
Đúng 0
Bình luận (0)
ai kết bạn với pika chu đi nè
Xem thêm câu trả lời
Cho tam giác ABC, trung tuyến AM, G là trọng tâm tam giác ABC. Gọi D và N lần lượt là trọng tâm của tam giác AMB và tam giác AMC. Chứng minh rằng 3 điểm D;G;N thẳng hàng?
ta gọi AH,AK là 2 đường trung tuyến của tam giác ABM và AMC
ta có D,G,N lần lượt là trọng tâm tam giác ABM,ABC,AM
=> \(\frac{AD}{AH}=\frac{AG}{AM}=\frac{AN}{AK}=\frac{2}{3}\) (tính chất trọng tâm)
=> DG//BC(đingj lí ta lét) và GN//BC(định lí ta lét )
=> D,G,N thẳng hàng(ĐPCM)
Đúng 0
Bình luận (0)
bạn ơi xem lại đề đi sao M lại là trọng tâm của tam giác AMB?
Đúng 0
Bình luận (0)
Cho tam giác ABC có trung tuyến AM. Lấy điểm G trên AM sao cho AG = 2GM
a) Chứng minh rằng G là trọng tâm của tam giác ABC
b) Gọi D, E, F lần lượt là hính chiếu của G trên các cạnh BC, CA, AB. Chứng minh rằng G cũng là trọng tâm của tam giác DEF



