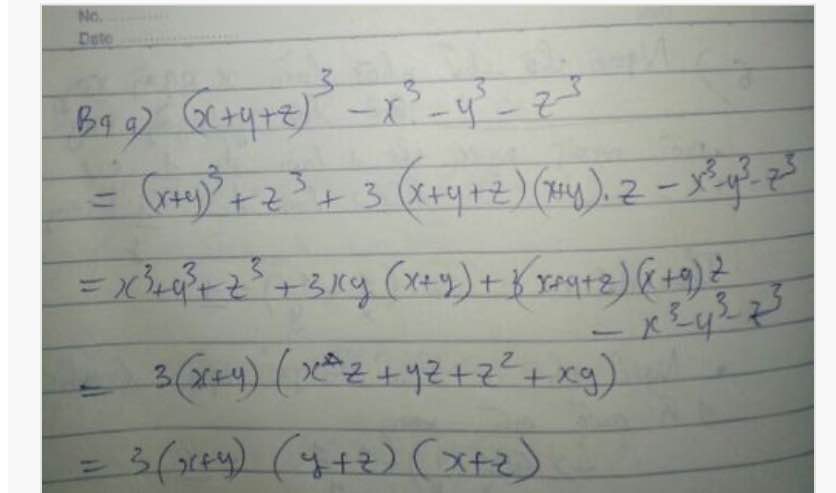Phân tích đa thức thành nhân tử: x + y + z 3 - z 3 - y 3 - z 3
PB
Những câu hỏi liên quan
Đa thức x^3 - 2x^2 + x - xy^2 được phân tích thành nhân tử
Đa thức x^3 + 3x^2y +3xy^2 + y^3 được phân tích thành nhân tử là
Đa thức 4x(2y-z)+7y(2y-z) được phân tích thành nhân tử là:
Đa thức x^2+4x+4 được phân tích thành nhân tử là
Tìm x biết x(x-2)-x+2
\(1,=x\left(x^2-2x+1-y^2\right)=x\left[\left(x-1\right)^2-y^2\right]=x\left(x-y-1\right)\left(x+y-1\right)\\ 2,=\left(x+y\right)^3\\ 3,=\left(2y-z\right)\left(4x+7y\right)\\ 4,=\left(x+2\right)^2\\ 5,Sửa:x\left(x-2\right)-x+2=0\\ \Leftrightarrow\left(x-2\right)\left(x-1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
Đúng 1
Bình luận (0)
phân tích đa thức đa thức sau thành nhân tử x+y+z = x^3-y^3-z^3
Phân tích đa thức thành nhân tử: (x+y+z)^3-x-y-z
\(\left(x+y+z\right)^3-x-y-z\\ =\left(x+y+z\right)^3-\left(x+y+z\right)\\ =\left(x+y+z\right)\left(\left(x+y+z\right)^2-1\right)\\ =\left(x+y+z\right)\left(x+y+z-1\right)\left(x+y+z+1\right)\)
Đúng 2
Bình luận (0)
Phân tích đa thức thành nhân tử:
8(x+y+z)3-(x+y)3-(y+z)3-(z+x)3
Đặt \(\left\{{}\begin{matrix}a=x+y\\b=y+z\\c=x+z\end{matrix}\right.\Leftrightarrow x+y+z=\dfrac{a+b+c}{2}\)
\(8\left(x+y+z\right)^3-\left(x+y\right)^3-\left(y+z\right)^3-\left(z+x\right)^3\\ =8\left(\dfrac{a+b+c}{2}\right)^3-a^3-b^3-c^3\\ =\left(a+b+c\right)^3-a^3-b^3-c^3\\ =\left(a+b\right)^3+c^3+3\left(a+b\right)c\left(a+b+c\right)-\left(a+b\right)^3+3ab\left(a+b\right)-c^3\\ =3\left(a+b\right)\left(ac+bc+c^2+ab\right)\\ =3\left(a+b\right)\left(b+c\right)\left(a+c\right)\\ =3\left(x+y+y+z\right)\left(y+z+z+x\right)\left(z+x+x+y\right)\\ =3\left(x+2y+z\right)\left(x+y+2z\right)\left(2x+y+z\right)\)
Đúng 1
Bình luận (0)
phân tích đa thức thành nhân tử :(x-y)z^3+(y-z)^3+(z-x)y^3
1.Đa thức 4x(2y-z) +7y(2y-z) được phân tích thành nhân tử là :
A .(2y+z)(4x+7y)
B.(2y-z)(4x-7y)
C.(2y+z)(4x-7y)
D. (2y-z)(4x+7y)
2 Phân tích đa thức x2+3x+xy+3y thành nhân tử ta được :
A. (x+3)(y+3)
B. (x-y)(x+3)
C. (x+3)(x+y)
D. Cả 3 đều sai
Phân tích đa thức thành nhân tử:
\(\left(x+y+z\right)^3-x^3-y^3-z^3\)
phân tích đa thức thành nhân tử (x+y+z)^3-x^3-y^3-z^3
\(\left(x+y+z\right)^3=x^3+y^3+z^3+\left(x+y\right)\left(x+z\right)\left(y+z\right)\)
\(\left(x+y+z\right)^3-x^3+y^3+z^3\)
\(=\left(x+y\right)\left(y+z\right)\left(x+z\right)\)
phân tích đa thức thành nhân tử : (x-y)^3 + (y-z)^3 + (z-x)^3
Ta có: (x-y)^3+(y-z)^3+(z-x)^3
Bạn để ý thấy (x-y)^3+(y-z)^3 là hằng đẳng thức dạng A^3+B^3=(A+B)(A^2-AB+B^2). Vậy ta có thể phân tích (x-y)^3+(y-z)^3 như sau
(x-y+y-z)((x-y)^2-(x-y)(y-z)+(y-z)^2)
(x-z)((x-y)^2-(x-y)(y-z)+(y-z)^2)
-(z-x)((x-y)^2-(x-y)(y-z)+(y-z)^2)
Đến đây thì bn đã có nhân tử chung là (z-x).
Đúng 0
Bình luận (0)
(x-y)^3+(y-z)^3+(z-x)^3
=(x-y+y-z)((x-y)^2-(x-y)(y-z)+(y-z)^2)
=(x-z)((x-y)^2-(x-y)(y-z)+(y-z)^2)
=-(z-x)((x-y)^2-(x-y)(y-z)+(y-z)^2)
.......
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử:(x+y+z)^3-(x+y-z)^3-(y+z-x)^3-(z+x-y)^3