TXĐ: D = R \ {-2}

Ta có: \(y'=\dfrac{\left(-2x+2\right)\left(x+2\right)-\left(-x^2+2x-1\right)}{\left(x+2\right)^2}=\dfrac{-x^2-4x+5}{\left(x+2\right)^2}\)

\(y'=0\Rightarrow-x^2-4x+5=0\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=1\end{matrix}\right.\)

⇒ Hàm số y đồng biến trên (-5, -2) và (-2, 1)

Hàm số y nghịch biến trên (-∞, -5) và (1, +∞)

TXĐ: [0; + ∞ )

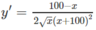
y’ = 0 ⇔ x = 100

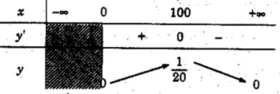
Vậy hàm số đồng biến trên khoảng (0; 100) và nghịch biến trên khoảng (100; + ∞ )

TXĐ: \(D=R\)

\(y'=\dfrac{-5x+8}{2\sqrt{\left(x^2-x+3\right)^3}}=0\Rightarrow x=\dfrac{8}{5}\)

Dấu của y' trên trục số:

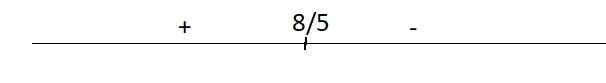
Từ đây ta thấy hàm đồng biến trên \(\left(-\infty;\dfrac{8}{5}\right)\) và nghịch biến trên \(\left(\dfrac{8}{5};+\infty\right)\)

\(f\left(x\right)=x+\sqrt[]{x^2-4}\)

\(f\left(x\right)\) xác định khi và chỉ khi

\(x^2-4\ge0\Leftrightarrow x^2\ge4\Leftrightarrow x\le-2\cup x\ge2\)

Tập xác định : \(D=(-\infty;-2]\cup[2;+\infty)\)

\(f'\left(x\right)=1+\dfrac{x}{\sqrt[]{x^2-4}}\)

\(f'\left(x\right)=0\)

\(\Leftrightarrow1+\dfrac{x}{\sqrt[]{x^2-4}}=0\)

\(\Leftrightarrow\dfrac{\sqrt[]{x^2-4}+x}{\sqrt[]{x^2-4}}=0\)

\(\Leftrightarrow\sqrt[]{x^2-4}+x=0\left(x< -2;x>2\right)\)

Theo bất đẳng thức Bunhiacopxki:

\(\left(1.\sqrt[]{x^2-4}+1.x\right)^2\le2\left(2x^2+4\right)=4\left(x^2+2\right)\)

\(pt\Leftrightarrow4\left(x^2+2\right)=0\left(vô.lý\right)\)

\(\Rightarrow\) phương trình vô nghiệm

Tiếp tục bài giải, mình nhấn nút gửi

\(...\Rightarrow f'\left(x\right)>0,\forall x\in D\)

\(\Rightarrow f\left(x\right)\) luôn luôn tăng trên tập xác định D.

cả nhà giúp mình với mai minh kiểm tra chất lượng rồi. Thanks all.