Trên đường tròn tâm O lấy ba điểm A, B, C sao cho A O B ^ = 100 o s đ A C ⏜ = 45 o . Tính số đo của cung nhỏ BC và cung lớn BC. (Xét cả hai trường hợp: điểm C nằm trên cung nhỏ AB, điểm C nằm trên cung lớn AB).
PB
Những câu hỏi liên quan
Cho đường tròn tâm O và điểm B trên đường tròn. Qua B kẻ tiếp tuyến với đường tròn trên đó lấy điểm A. Trên AO lấy điểm C sao cho AC =BA. Tia BC cắt tâm O ở E. Chứng minh: OE vuông góc vs OA
Vì tam giác ABC cân tại A nên \(\widehat{ACB}=\widehat{ABC}\)
Lại có \(\widehat{ACB}\) và \(\widehat{OCE}\) là hai góc đối đỉnh nên chúng bằng nhau. Nói cách khác \(\widehat{OCE}=\widehat{ABC}\)
Do OE = OB nên \(\widehat{OEB}=\widehat{OBE}\)
Mà \(\widehat{ABC}+\widehat{OBE}=90^o\Rightarrow\widehat{OCE}+\widehat{OEB}=90^o\Rightarrow\widehat{EOC}=90^o.\)
Vậy \(OE\perp OA.\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Cho đường tròn tâm O và điểm B trên đường tròn. Qua B kẻ tiếp tuyến với đường tròn trên đó lấy điểm A. Trên AO lấy điểm C sao cho AC=BA. Tia BC cắt tâm O ở E. Chứng minh: OE vuông góc OA.
Cho đường tròn tâm O và điểm B trên đường tròn. Qua B kể tiếp tuyến đường tròn trên đó lấy điểm A. Trên AO lấy điểm C sao cho AC=BA. Tia BC cắt tâm ở E. Chứng minh:OE vuông góc OA
Trên đường tròn tâm O lấy ba điểm A, B, C sao cho
A
O
B
^
100
°
sd
A
C
^
45
°
. Tính số đo của cung nhỏ BC và cung lớn BC. (Xét cả hai trường hợp: điểm C nằm trên cung nhỏ AB, điểm C nằm trên cun...
Đọc tiếp
Trên đường tròn tâm O lấy ba điểm A, B, C sao cho A O B ^ = 100 ° sd A C ^ = 45 ° . Tính số đo của cung nhỏ BC và cung lớn BC. (Xét cả hai trường hợp: điểm C nằm trên cung nhỏ AB, điểm C nằm trên cung lớn AB).
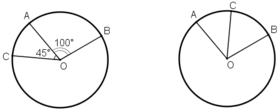
* Trường hợp 1 . Điểm C nằm trên cung lớn AB.
Do điểm C nằm trên cung lớn AB nên tia OA nằm giữa hai tia OB và OC.
Do ![]() nên tia OA nằm giữa hai tia OB và OC hay A nằm trên cung BC.
nên tia OA nằm giữa hai tia OB và OC hay A nằm trên cung BC.
Suy ra: ![]() =
100
0
+
45
0
=
145
0
=
100
0
+
45
0
=
145
0
Khi đó, số đo cung nhỏ BC là
145
°
( bằng góc ở tâm 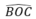 )
)
Số đo cung lớn BC là: 360 0 − 145 0 = 215 0
* Trường hợp 2: Điểm C nằm trên cung nhỏ AB
Vì điểm C nằm trên cung nhỏ AB nên OC nằm giữa OA và OB
![]()
Ta có: ![]() =
100
0
−
45
0
=
55
0
=
100
0
−
45
0
=
55
0
Khi đó, số đo cung nhỏ BC là 55 0
Số đo cung lớn BC là: 360 0 − 55 0 = 305 0
Kiến thức áp dụng
+ Góc có đỉnh trùng với tâm đường tròn được gọi là góc ở tâm.
+ Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
+ Số đo của cung lớn bằng hiệu của 360º và số đo của cung nhỏ (có chung hai mút với cung lớn).
Đúng 1
Bình luận (0)
Cho đường tròn tâm O, bán kính R; dây AB=R. Trên tia đối của tia BA lấy điểm C sao cho BC=BA. Tia CO cắt đường tròn tâm O ở D; biết D=3.
a) Tính góc ACD
b) Tính CD
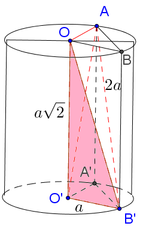
Cho hình trụ có các đáy là hai hình tròn tâm O và O’, bán kính đáy bằng a, chiều cao bằng
a
2
. Trên đường tròn đáy tâm O lấy điểm A, trên đường tròn đáy tâm O’ lấy điểm O sao cho AB 2a. Tính thể tích của khối tứ diện OO′B′A. A.
a
3
3
2
B.
a
3...
Đọc tiếp
Cho hình trụ có các đáy là hai hình tròn tâm O và O’, bán kính đáy bằng a, chiều cao bằng a 2 . Trên đường tròn đáy tâm O lấy điểm A, trên đường tròn đáy tâm O’ lấy điểm O' sao cho AB' = 2a. Tính thể tích của khối tứ diện OO′B′A.
A. a 3 3 2
B. a 3 2 12
C. a 3 2 6
D. a 3 6
Cho hình trụ có các đáy là 2 hình tròn tâm O và O, bán kính đáy bằng chiều cao vào bằng a. Trên đường tròn đáy tâm O lấy điểm A, trên đường tròn tâm O lấy điểm B sao cho AB2a. Thể tích khối tứ diện OOAB theo a là A.
V
3
a
3
8
B.
V
3...
Đọc tiếp
Cho hình trụ có các đáy là 2 hình tròn tâm O và O', bán kính đáy bằng chiều cao vào bằng a. Trên đường tròn đáy tâm O lấy điểm A, trên đường tròn tâm O lấy điểm B sao cho AB=2a. Thể tích khối tứ diện OO'AB theo a là
A. V = 3 a 3 8
B. V = 3 a 3 4 .
C. V = 3 a 3 6 .
D. V = 3 a 3 12 .
Cho đường tròn tâm O đường kính AB , trên cùng một nửa đường tròn ( O ) lấy 2 điểm G và E ( theo thứ tự A , C , E , B ) sao cho tỉa IG cắt tia BA tại D. Duong thẳng vuông góc với BD tại D cắt BD tại C , đường thăng C1 cặt đường tròn ( O ) tại điểm thứ hai là F. a ) Chứng minh tỉ giác DFBC nội tiếp . b ) Chứng minh : BF = BG b ) Chủng minh : DA DGDE BA BE BC
Cho đường tròn tâm O, đường kính AB và d là một tiếp tuyến của đường tròn (O) tại điểm A. Trên đường thẳng d lấy điểm M (khác A) và trên đoạn OB lấy điểm N (khác O và B). Đường thẳng MN cắt đường tròn (O) tại hai điểm C và D sao cho C nằm giữa M và D. Gọi H là trung điểm của đoạn thẳng CD.a) Chứng minh tứ giác AOHM nội tiếp được trong đường tròn.c) Đường thẳng BC cắt đường thẳng OM tại I. Chứng minh rằng đường thẳng AI song song với đường thẳng BD.
Đọc tiếp
Cho đường tròn tâm O, đường kính AB và d là một tiếp tuyến của đường tròn (O) tại điểm A. Trên đường thẳng d lấy điểm M (khác A) và trên đoạn OB lấy điểm N (khác O và B). Đường thẳng MN cắt đường tròn (O) tại hai điểm C và D sao cho C nằm giữa M và D. Gọi H là trung điểm của đoạn thẳng CD.
a) Chứng minh tứ giác AOHM nội tiếp được trong đường tròn.
c) Đường thẳng BC cắt đường thẳng OM tại I. Chứng minh rằng đường thẳng AI song song với đường thẳng BD.
Cho đường tròn tâm O, đường kính AB và d là một tiếp tuyến của đường tròn (O) tại điểm A. Trên đường thẳng d lấy điểm M (khác A) và trên đoạn OB lấy điểm N (khác O và B). Đường thẳng MN cắt đường tròn (O) tại hai điểm C và D sao cho C nằm giữa M và D. Gọi H là trung điểm của đoạn thẳng CD.a) Chứng minh tứ giác AOHM nội tiếp được trong đường tròn. c) Đường thẳng BC cắt đường thẳng OM tại I. Chứng minh rằng đường thẳng AI song song với đường thẳng BD.
Đọc tiếp
Cho đường tròn tâm O, đường kính AB và d là một tiếp tuyến của đường tròn (O) tại điểm A. Trên đường thẳng d lấy điểm M (khác A) và trên đoạn OB lấy điểm N (khác O và B). Đường thẳng MN cắt đường tròn (O) tại hai điểm C và D sao cho C nằm giữa M và D. Gọi H là trung điểm của đoạn thẳng CD.
a) Chứng minh tứ giác AOHM nội tiếp được trong đường tròn.
c) Đường thẳng BC cắt đường thẳng OM tại I. Chứng minh rằng đường thẳng AI song song với đường thẳng BD.