Hệ bất phương trình x 2 - 4 x + 3 > 0 x 2 - 6 x + 8 > 0 có tập nghiệm là
A.( - ∞ ;1) ∪ (3; + ∞ )
B. ( - ∞ ;1) ∪ (4; + ∞ )
C. ( - ∞ ;2) ∪ (3; + ∞ )
D. (1;4)
PB
Những câu hỏi liên quan
Cho hệ bất phương trình:
x
+
m
≤
0
x
2
-
x
+
4
x
2...
Đọc tiếp
Cho hệ bất phương trình:
x + m ≤ 0 x 2 - x + 4 < x 2 - 1
Hệ bất phương trình đã cho có nghiệm khi và chỉ khi
A. m < –5
B. m > –5
C. m > 5
D. m < 5
Chọn B.
Xét hệ bất phương trình:
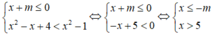
Để hệ bất phương trình có nghiệm thì 5 < -m ⇔ m > -5.
Đúng 0
Bình luận (0)
Cho hệ bất phương trình sau: \(\left\{ \begin{array}{l}x - 2y \ge - 2\\7x - 4y \le 16\\2x + y \ge - 4\end{array} \right.\)
a) Trong cùng mặt phẳng toạ độ Oxy, biểu diễn miền nghiệm của mỗi bất phương trình
trong hệ bất phương trình bằng cách gạch bỏ phần không thuộc miền nghiệm của nó.
b) Tìm miền nghiệm của hệ bất phương trình đã cho.
a) Trong cùng mặt phẳng toạ độ Oxy, vẽ ba đường thẳng:
\({d_1}:x - 2y = - 2\);
\({d_2}:7x - 4y = 16\)
\({d_3}:2x + y = - 4\)
Thay tọa độ điểm O vào \(x - 2y\) ta được:
\(0 - 2.0 = 0 \ge - 2\)
=> Điểm O thuộc miền nghiệm
=> Gạch phần không chứa điểm O.
Thay tọa độ điểm O vào \(7x - 4y\) ta được:
\(7.0 - 4.0 = 0 \le 16\)
=> Điểm O thuộc miền nghiệm
=> Gạch phần không chứa điểm O.
Thay tọa độ điểm O vào \(2x + y\) ta được:
\(2.0 + 0 = 0 \ge - 4\)
=> Điểm O thuộc miền nghiệm
=> Gạch phần không chứa điểm O.
b)
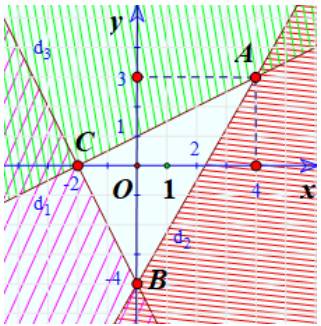
Miền nghiệm của hệ là phần không bị gạch bỏ chung của cả 3 miền nghiệm trên.
Chú ý
Ở câu a, có thể thay điểm O bằng các điểm khác.
Đúng 0
Bình luận (0)
Cho hệ bất phương trình 0≤ x ≤ 4; 0 ≤ y ≤ 5; y - x ≥ 3
a. Biểu diễn tập nghiệm của hệ bất phương trình trên hệ trục Oxy
b. Tìm giá trị lớn nhất của biểu thức S= 2x + y
Bài 1: Tìm m sao cho hệ bất phương trình \(\left\{{}\begin{matrix}x^2-3x-4\le0\\\left(m-1\right)x-2\ge0\end{matrix}\right.\)có nghiệm.
Bài 2: Tìm tất cả giá trị thực của tham số m để hệ bất phương trình \(\left\{{}\begin{matrix}x^2+10x+16\le0\\mx\ge3x+1\end{matrix}\right.\)vô nghiệm.
Bài 1 \(\left\{{}\begin{matrix}x^2-3x-4\le0\\\left(m-1\right)x\ge2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-1\le x\le4\\\left(m-1\right)x\ge2\end{matrix}\right.\)
Nếu m = 1, hệ vô nghiệm
Nếu m ≠ 1, hệ tương đương
\(\left[{}\begin{matrix}\left\{{}\begin{matrix}-1\le m< 1\\x\le\dfrac{2}{m-1}\end{matrix}\right.\\\left\{{}\begin{matrix}1< m\le4\\x\ge\dfrac{2}{m-1}\end{matrix}\right.\end{matrix}\right.\)
Hệ có nghiệm khi một trong hai hệ trong hệ ngoặc vuông có nghiệm ⇔ \(\left[{}\begin{matrix}\left\{{}\begin{matrix}-1\le m< 1\\\dfrac{2}{m-1}\ge-1\end{matrix}\right.\\\left\{{}\begin{matrix}1< m\le4\\\dfrac{2}{m-1}\le4\end{matrix}\right.\end{matrix}\right.\)
⇔ \(\left[{}\begin{matrix}\left\{{}\begin{matrix}-1\le m< 1\\-2\le1-m\end{matrix}\right.\\\left\{{}\begin{matrix}1< m\le4\\2\le4m-4\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}-1\le m< 1\\\dfrac{3}{2}\le m\le4\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho hệ bất phương trình
x
+
m
≤
0
1
x
2
-
x
+
4...
Đọc tiếp
Cho hệ bất phương trình x + m ≤ 0 1 x 2 - x + 4 < x 2 - 1 2
Hệ đã cho có nghiệm khi và chỉ khi
A. m<-5
B. m>-5
C. m>5
D. m<5
Giải các bất phương trình, hệ bất phương trình (ẩn m) sau:
(
2
m
-
1
)
2
-
4
(
m
+
1
)
(
m
-
2
)
≥
0
Đọc tiếp
Giải các bất phương trình, hệ bất phương trình (ẩn m) sau:
( 2 m - 1 ) 2 - 4 ( m + 1 ) ( m - 2 ) ≥ 0
( 2 m - 1 ) 2 - 4 ( m + 1 ) ( m - 2 ) ≥ 0 ⇔ 9 ≥ 0. Bất phương trình có tập nghiệm là R.
Đúng 0
Bình luận (0)
Tìm tất cả tham số `m` để bất phương trình `x^2-x+m(1-m)<=0` là hệ quả của bất phương trình `\sqrt{\sqrt{x-1}+4}-\sqrt{\sqrt{x-1}+1}>=1`?
`A.m=1/2`
`B.m<=0` hoặc `m>=1`
`C.m>=1`
`D.m<=0`
Với m = 1/2 thì bpt (1) \(\Leftrightarrow\left(x-\dfrac{1}{2}\right)^2\le0\Leftrightarrow x=\dfrac{1}{2}\)
bpt(2) \(\sqrt{\sqrt{x-1}+4}-\sqrt{\sqrt{x-1}+1}\ge1\) ( ĐK : \(x\ge1\) )
\(\Leftrightarrow\sqrt{\sqrt{x-1}+4}\ge1+\sqrt{\sqrt{x-1}+1}\)
\(\Leftrightarrow\sqrt{x-1}+4\ge1+\sqrt{x-1}+1+2\sqrt{\sqrt{x-1}+1}\)
\(\Leftrightarrow2\ge2\sqrt{\sqrt{x-1}+1}\Leftrightarrow1\ge\sqrt{\sqrt{x-1}+1}\) \(\Leftrightarrow\sqrt{x-1}+1\le1\Leftrightarrow\sqrt{x-1}\le0\Leftrightarrow x=1\)
bpt (2) có no x = 1 . Loại A
Với m khác 1/2 \(x^2-x+m\left(1-m\right)\le0\)
\(\Leftrightarrow x^2-m^2-\left(x-m\right)\le0\) \(\Leftrightarrow\left(x-m\right)\left(x+m-1\right)\le0\)
\(\Leftrightarrow\left[{}\begin{matrix}x\ge m;x\le1-m\\x\le m;x\ge1-m\end{matrix}\right.\)
Vì bpt (1) là hệ quả bpt (2) nên bpt (1) có no x = 1
Khi đó : \(\left[{}\begin{matrix}1\ge m;1\le1-m\\1\le m;1\ge1-m\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m\le0\\m\ge1\end{matrix}\right.\)
Chọn B
Đúng 2
Bình luận (0)
Tìm tất cả tham số mm để bất phương trình x2−x+m(1−m)≤0x2-x+m(1-m)≤0 là hệ quả của bất phương trình √√x−1+4−√√x−1+1≥1x-1+4-x-1+1≥1?
A.m=12A.m=12
B.m≤0B.m≤0 hoặc m≥1m≥1
C.m≥1C.m≥1
D.m≤0D.m≤0
Đúng 1
Bình luận (0)
Cho hệ bất phương trình
m
x
2
-
x
-
5
≤
0
(
1
-
m
)
x...
Đọc tiếp
Cho hệ bất phương trình m x 2 - x - 5 ≤ 0 ( 1 - m ) x 2 + 2 m x + m + 2 ≥ 0 . Các giá trị của x thỏa mãn hệ bất phương trình khi m = 1 là:
A. S = 1 - 2 21 2 ; 1 + 2 21 2
B. S = 1 - 3 21 2 ; 1 + 3 21 2
C. S = 1 - 4 21 2 ; 1 + 4 21 2
D. S = 1 - 21 2 ; 1 + 21 2
Chọn D.
Với m = 1 hệ bất phương trình trở thành:
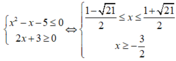
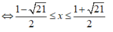
Vậy tập nghiệm hệ bất phương trình là
Đúng 0
Bình luận (0)
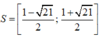
Cho hệ bất phương trình\(\left\{{}\begin{matrix}x^2-3x-4\le0\\x^2-3\left|x\right|x-m^2+6m\ge0\end{matrix}\right.\) . Tìm m để hệ có nghiệm
Hệ bất phương trình
(
x
+
3
)
(
4
-
x
)
0
x
m...
Đọc tiếp
Hệ bất phương trình ( x + 3 ) ( 4 - x ) > 0 x < m - 1 vô nghiệm khi
A. m ≤ -2
B. m > -2
C. m < 1
D. m > 2
Chọn A
Ta có:
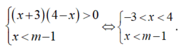
Hệ bất phương trình vô nghiệm khi và chỉ khi m-1≤ -3 hay m≤ - 2.
Đúng 0
Bình luận (0)