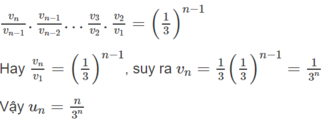Cho dãy số ( u n ) là một cấp số nhân có số hạng đầu u 1 = 1 , công bội q = 2 . Tính tổng T = 1 u 1 - u 5 + 1 u 2 - u 6 + 1 u 3 - u 7 + . . . + 1 u 20 - u 24
A. 1 - 2 19 15 . 2 18
B. 1 - 2 20 15 . 2 19
C. 2 19 - 1 15 . 2 18
D. 2 20 - 1 15 . 2 19
PB
Những câu hỏi liên quan
Cho dãy số \({u_n}\)với \({u_n} = {2.5^n}\). Chứng minh rằng dãy số này là một cấp số nhân. Xác định số hạng đầu và công bội của nó.
Ta có: \(\frac{{{u_n}}}{{{u_{n - 1}}}} = \frac{{2 \times {5^n}}}{{2 \times {5^{n - 1}}}} = \frac{{2 \times {5^n}}}{{2 \times {5^{n}.5^{- 1}}}} = 5,\;\forall n \ge 2\).
Vậy dãy số \(\left( {{u_n}} \right)\) là một cấp số nhân với \({u_1} = 10\) và công bội \(q = 5\).
Đúng 0
Bình luận (0)
1) cho dãy số có các số hạng đầu là 8; 15;22; 29; 36;.. số hạng tổng quát của dãy số là2) cho cấp số cộng left(u_nright) với u_12;d9. Khi đó số 2018 là số hạng thứ mấy của dãy3) cho cấp số nhân left(u_nright) có u_15;q2. Số hạng thứ 6 của cấp số nhân là4) cho cấp số nhân left(u_nright) có u_12;u_26.Công bội của cấp số nhân bằng
Đọc tiếp
1) cho dãy số có các số hạng đầu là 8; 15;22; 29; 36;.. số hạng tổng quát của dãy số là
2) cho cấp số cộng \(\left(u_n\right)\) với \(u_1=2;d=9\). Khi đó số 2018 là số hạng thứ mấy của dãy
3) cho cấp số nhân \(\left(u_n\right)\) có \(u_1=5;q=2\). Số hạng thứ 6 của cấp số nhân là
4) cho cấp số nhân \(\left(u_n\right)\) có \(u_1=2;u_2=6\).Công bội của cấp số nhân bằng
Cho một cấp số nhân có n số hạng. Số hạng đầu tiên là 1, công bội là q và tổng là S. Trong đó q và S đều khác 0. Tổng các số hạng của cấp số nhân mới được thành bằng cách thay đổi mỗi số hạng của cấp số nhân ban đầu bằng nghịch đảo của nó là: A.
1
S
.
B.
1
q
n
.
S...
Đọc tiếp
Cho một cấp số nhân có n số hạng. Số hạng đầu tiên là 1, công bội là q và tổng là S. Trong đó q và S đều khác 0. Tổng các số hạng của cấp số nhân mới được thành bằng cách thay đổi mỗi số hạng của cấp số nhân ban đầu bằng nghịch đảo của nó là:
A. 1 S .
B. 1 q n . S .
C. S q n − 1 .
D. q n S .
Đáp án C
Em có: S = 1. q n − 1 q − 1 = q n − 1 q − 1 .
Vì cấp số nhân mới tạo thành bằng cách thay đổi mỗi số hạng của cấp số nhân ban đầu thành nghịch đảo của nó nên cấp số nhân mới sẽ có công bội là 1 q .
Gọi S' là tổng mới của cấp số nhân mới.
Em có: S ' = 1 q n − 1 1 q − 1 = 1 − q n q n . 1 − q q = 1 − q n 1 − q . 1 q n − 1 = S q n − 1 .
Vậy tổng của cấp số nhân mới là: S q n − 1 .
Đúng 0
Bình luận (0)
Cho dãy số
u
n
là một cấp số cộng có
u
1
3
và công sai d4. Biết tổng n số hạng đầu của dãy số
u
n
là
S
n
253
. Tìm n? A. 10 B. 9 C. 12 D. 11
Đọc tiếp
Cho dãy số u n là một cấp số cộng có u 1 = 3 và công sai d=4. Biết tổng n số hạng đầu của dãy số u n là S n = 253 . Tìm n?
A. 10
B. 9
C. 12
D. 11
Cho một dãy số có các số hạng đầu tiên là 1,8,22,43...Hiệu của hai số hạng liên tiếp của dãy số đó lập thành một cấp số cộng: 7,14,21,...,7n. Số 35351 là số hạng thứ bao nhiêu của dãy số đã cho?
A. 57
B. 80
C. 101
D. 200
Chọn C
Theo đề bài ta có:
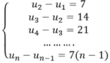
Cộng vế với vế các phương trình của hệ ta được:
Đúng 0
Bình luận (0)
Cho dãy số
u
n
là một cấp số nhân có số hạng đầu
u
1
1
, công bội q 2 . Tính tổng
T
1
u
1
-
u
5
+
1
u
2...
Đọc tiếp
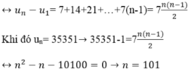
Cho dãy số u n là một cấp số nhân có số hạng đầu u 1 = 1 , công bội q = 2 . Tính tổng T = 1 u 1 - u 5 + 1 u 2 - u 6 + 1 u 3 - u 7 + . . . + 1 u 20 - u 24
A. 1 - 2 19 15 . 2 18
B. 1 - 2 20 15 . 2 19
C. 2 19 - 1 15 . 2 18
D. 2 20 - 1 15 . 2 19
Câu 1:
Cho một dãy số có các số hạng đầu tiên là 1,8,22,43,..... Hiệu của 2 số hạng liên tiếp của dãy đó lập thành một cấp số cộng: 7,14,21,...7n. Số 35351 là số hạng thứ mấy của cấp số đã cho?
Câu 2:
Cho tam giác ABC, có 3 cạnh a,b,c theo thứ tự lập thành 1 cấp số cộng. Tính giá trị biểu thức P cotdfrac{A}{2}. cot dfrac{C}{2}
Câu 3:
Cho 2 cấp số cộng hữu hạn, mỗi cấp số có 100 số hạng:4,7,10,13,16,... và 1,6,11,16,21,... Hỏi có tất cả bao nhiêu số có mặt trong cả 2 cấp số trên?
Đọc tiếp
Câu 1:
Cho một dãy số có các số hạng đầu tiên là 1,8,22,43,..... Hiệu của 2 số hạng liên tiếp của dãy đó lập thành một cấp số cộng: 7,14,21,...7n. Số 35351 là số hạng thứ mấy của cấp số đã cho?
Câu 2:
Cho tam giác ABC, có 3 cạnh a,b,c theo thứ tự lập thành 1 cấp số cộng. Tính giá trị biểu thức P= cot\(\dfrac{A}{2}\). cot \(\dfrac{C}{2}\)
Câu 3:
Cho 2 cấp số cộng hữu hạn, mỗi cấp số có 100 số hạng:4,7,10,13,16,... và 1,6,11,16,21,... Hỏi có tất cả bao nhiêu số có mặt trong cả 2 cấp số trên?
Câu 1:
Dãy đã cho có thể viết dưới dạng công thức truy hồi sau:
\(\left\{{}\begin{matrix}u_1=1\\u_{n+1}=u_n+7n\end{matrix}\right.\)
\(u_{n+1}=u_n+7n\Leftrightarrow u_{n+1}-\dfrac{7}{2}\left(n+1\right)^2+\dfrac{7}{2}\left(n+1\right)=u_n-\dfrac{7}{2}n^2+\dfrac{7}{2}n\)
Đặt \(v_n=u_n-\dfrac{7}{2}n^2+\dfrac{7}{2}n\Rightarrow\left\{{}\begin{matrix}v_1=1\\v_{n+1}=v_n\end{matrix}\right.\)
\(\Rightarrow v_{n+1}=v_n=v_{n-1}=...=v_1=1\)
\(\Rightarrow u_n-\dfrac{7}{2}n^2+\dfrac{7}{2}n=1\)
\(\Leftrightarrow u_n=\dfrac{7}{2}n^2-\dfrac{7}{2}n+1\)
\(\dfrac{7}{2}n^2-\dfrac{7}{2}n+1=35351\)
\(\Leftrightarrow\dfrac{7}{2}n^2-\dfrac{7}{2}n-35350=0\)
\(\Rightarrow n=101\)
Vậy đó là số hạng thứ 101
Đúng 1
Bình luận (0)
2.
Do a;b;c lập thành 1 cấp số cộng
\(\Rightarrow a+c=2b\)
\(\Leftrightarrow2R.sinA+2R.sinC=2.2R.sinB\)
\(\Leftrightarrow sinA+sinC=2sinB\)
\(\Leftrightarrow2sin\dfrac{A+C}{2}.cos\dfrac{A-C}{2}=4sin\dfrac{B}{2}cos\dfrac{B}{2}\)
\(\Leftrightarrow cos\dfrac{B}{2}cos\dfrac{A-C}{2}=2sin\dfrac{B}{2}cos\dfrac{B}{2}\)
\(\Leftrightarrow cos\dfrac{A-C}{2}=2sin\dfrac{B}{2}=2cos\dfrac{A+C}{2}\)
\(\Leftrightarrow cos\left(\dfrac{A}{2}\right)cos\left(\dfrac{C}{2}\right)+sin\left(\dfrac{A}{2}\right)sin\left(\dfrac{C}{2}\right)=2cos\left(\dfrac{A}{2}\right)cos\left(\dfrac{C}{2}\right)-2sin\left(\dfrac{A}{2}\right)sin\left(\dfrac{C}{2}\right)\)
\(\Leftrightarrow cos\left(\dfrac{A}{2}\right).cos\left(\dfrac{C}{2}\right)=3sin\left(\dfrac{A}{2}\right).sin\left(\dfrac{C}{2}\right)\)
\(\Leftrightarrow cot\left(\dfrac{A}{2}\right).cot\left(\dfrac{C}{2}\right)=3\)
Đúng 1
Bình luận (0)
3.
Công thức số hạng tổng quát của dãy đầu: \(u_n=4+3\left(n-1\right)=3n+1\)
Với \(1\le n\le100\)
Công thức số hạng tổng quát của dãy sau: \(v_m=1+5\left(m-1\right)=5m-4\)
Với \(1\le m\le100\)
Các số hạng của 2 dãy trùng nhau khi:
\(3n+1=5m-4\)
\(\Leftrightarrow5m=3n+5\Leftrightarrow m=\dfrac{3n}{5}+1\)
\(\Rightarrow n⋮5\Rightarrow n=5k\)
Mà \(1\le n\le100\Rightarrow1\le5k\le100\Rightarrow1\le k\le20\)
\(\Rightarrow\) Hai dãy số có 20 số hạng trùng nhau
Vậy số số có mặt trong 2 dãy trên là: \(100+100-20=180\) số
Đúng 1
Bình luận (0)
Cho cấp số nhân
u
n
có tổng n số hạng đầu tiên là
S
n
5
n
−
1
,
n
1
,
2
,
3
...
Tìm số hạng đầu
u
1
và công bội q của cấp số nhân đó. A.
u
1
5...
Đọc tiếp
Cho cấp số nhân u n có tổng n số hạng đầu tiên là S n = 5 n − 1 , n = 1 , 2 , 3 ... Tìm số hạng đầu u 1 và công bội q của cấp số nhân đó.
A. u 1 = 5 , q = 6
B. u 1 = 4 , q = 5
C. u 1 = 5 , q = 4
D. u 1 = 6 , q = 5
Cho dãy số
u
1
1
3
u
n
+
1
...
Đọc tiếp
Cho dãy số u 1 = 1 3 u n + 1 = n + 1 u n 3 n v ớ i n ≥ 1
a) Viết năm số hạng đầu của dãy số.
b) Lập dãy số ( v n ) với v n = u n n . Chứng minh dãy số ( v n ) là cấp số nhân.
c) Tìm công thức tính ( u n ) theo n.
a) Năm số hạng đầu là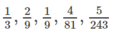 
b) Lập tỉ số
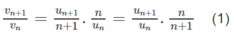
Theo công thứcđịnh nghĩa ta có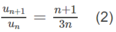 
Từ (1) và (2) suy ra
Vậy, dãy số ( v n ) là cấp số nhân, có v 1 = 1 / 3 , q = 1 / 3
c) Để tính ( u n ) , ta viết tích của n - 1 tỉ số bằng 1/3
Đúng 0
Bình luận (0)