Cho phép thử có không gian mẫu {1,2,3,4,5,6}Các cặp biến cố không đối nhau là
Đọc tiếp
Cho phép thử có không gian mẫu 
={1,2,3,4,5,6}Các cặp biến cố không đối nhau là
PB
Những câu hỏi liên quan
Cho phép thử có không gian mẫu
Ω
1
,
2
,
3
,
4
,
5
,
6
. Các cặp biến cố không đối nhau là A. C{1,4,5} và D {2,3,6}. B. E {1,4,6} và F {2,3,}. C.
Ω
và
∅
. D. A {1} và B {2,3,4,5,6}.
Đọc tiếp
Cho phép thử có không gian mẫu Ω = 1 , 2 , 3 , 4 , 5 , 6 . Các cặp biến cố không đối nhau là
A. C{1,4,5} và D = {2,3,6}.
B. E = {1,4,6} và F = {2,3,}.
C. Ω và ∅ .
D. A = {1} và B = {2,3,4,5,6}.
Xét một phép thử có không gian mẫu
Ω
và A là một biến cố của phép thử đó. Phát biểu nào dưới đây là sai? A. P(A) 0 khi và chỉ khi A là chắc chắn B.
0
≤
P
A
≤
1
C. Xác suất của biến cố A là số
P
A
n
A
n
Ω...
Đọc tiếp
Xét một phép thử có không gian mẫu Ω và A là một biến cố của phép thử đó. Phát biểu nào dưới đây là sai?
A. P(A) = 0 khi và chỉ khi A là chắc chắn
B. 0 ≤ P A ≤ 1
C. Xác suất của biến cố A là số P A = n A n Ω
D. P A = 1 - P A
Đáp án A
Các phát biểu B, C và D là đúng; phát biểu A là sai
Đúng 0
Bình luận (0)
Xét một phép thử có không gian mẫu
Ω
và
A
là một biến cố của phép thử đó. Phát biểu nào dưới đây là sai? A. P(A) 0 khi và chỉ khi A là chắc chắn B.
0
≤
P
(
A
)
≤
1
C. Xác suất của biến cố
A
là số ...
Đọc tiếp
Xét một phép thử có không gian mẫu Ω và A là một biến cố của phép thử đó. Phát biểu nào dưới đây là sai?
A. P(A) = 0 khi và chỉ khi A là chắc chắn
B. 0 ≤ P ( A ) ≤ 1
C. Xác suất của biến cố A là số P ( A ) = n ( A ) n ( Ω )
D. P ( A ) = 1 - P ( A ¯ )
Đáp án A
Các phát biểu B, C và D là đúng; phát biểu A là sai
Đúng 0
Bình luận (0)
Xét một phép thử có không gian mẫu
Ω
và A là một biến cố của phép thử đó. Phát biểu nào sau đây sai? A. Xác suất của biến cố A là
P
A
n
A
n
Ω
.
B.
0
≤
P
A
≤
1
.
C. ...
Đọc tiếp
Xét một phép thử có không gian mẫu Ω và A là một biến cố của phép thử đó. Phát biểu nào sau đây sai?
A. Xác suất của biến cố A là P A = n A n Ω .
B. 0 ≤ P A ≤ 1 .
C. P A = 1 - P A ¯ .
D. P A = 0 khi và chỉ khi A là biến cố chắc chắn.
Xét một phép thử có không gian mẫu
Ω
và A là một biến cố của phép thử đó. Phát biểu nào sau đây sai ? A. Xác suất của biến cố A là P(A)
n
(
A
)
n
(
Ω
)
B. 0
≤
P(A)1 C. P(A) 1 -
P
(
A
¯...
Đọc tiếp
Xét một phép thử có không gian mẫu Ω và A là một biến cố của phép thử đó. Phát biểu nào sau đây sai ?
A. Xác suất của biến cố A là P(A) = n ( A ) n ( Ω )
B. 0 ≤ P(A)1
C. P(A) = 1 - P ( A ¯ ) .
D. P(A) = 0 khi và chỉ khi A là biến cố chắc chắn.
Chọn D
Theo định nghĩa biến cố chắc chắn ta có: Với A là biến cố chắc chắn thì n(A) = n( Ω )
Suy ra: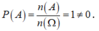 
.
Đúng 0
Bình luận (0)
Gọi n(A) là số các kết quả thuận lợi cho biến cố liên quan đến một phép thử T và
n
(
Ω
)
là số các kết quả có thể xảy ra của phép thử T đó. Xác suất P(
A
¯
) của biến cố đối của biến cố A không là đẳng thức nào trong các đẳng thức sau? A. P(
A
¯
)
n
(
A
)...
Đọc tiếp
Gọi n(A) là số các kết quả thuận lợi cho biến cố liên quan đến một phép thử T và n ( Ω ) là số các kết quả có thể xảy ra của phép thử T đó. Xác suất P( A ¯ ) của biến cố đối của biến cố A không là đẳng thức nào trong các đẳng thức sau?
A. P( A ¯ ) = n ( A ) n ( Ω )
B. P( A ¯ ) = 1 - P(A)
C. P( A ¯ ) = n ( A ¯ ) n ( Ω )
D. P( A ¯ ) = n ( Ω \ A ) n ( Ω )
Xét phép thử “Gieo một xúc xắc hai lần liên tiếp”.
a) Sự kiện “Số chấm trong lần gieo thứ hai là 6” tương ứng với biến cố nào của phép thử trên?
b) Phát biểu biến cố E={(5;6); 6;5); 6;6)} của không gian mẫu (trong phép thử trên) dưới dạng mệnh đề nêu sự kiện.
a) Sự kiện “Số chấm trong lần gieo thứ hai là 6” tương ứng với biến cố nào của phép thử
\(A{\rm{ }} = {\rm{ }}\left\{ {\left( {{\rm{1 }};{\rm{ 6}}} \right);{\rm{ }}\left( {{\rm{2 }};{\rm{ 6}}} \right);{\rm{ }}\left( {{\rm{3 }};6} \right);{\rm{ }}\left( {{\rm{4 }};{\rm{ 6}}} \right);{\rm{ }}\left( {{\rm{5 }};{\rm{ 6}}} \right);{\rm{ }}\left( {6{\rm{ }};{\rm{ }}6} \right)} \right\}\)
b) Biến cố E={(5;6); 6;5); 6;6)} của không gian mẫu (trong phép thử trên) được phát biểu dưới dạng mệnh đề nêu sự kiện là: “Tổng số chấm xuất hiện trong hai lần gieo không bé hơn 11”
Đúng 0
Bình luận (0)
Gieo đồng thời 1 đồng xu và 1 con xúc xắc. Hãy mô tả không gian mẫu của phép thử và tính xác suất của biến cố A : "Đồng xu xuất hiện mặt sấp và số chấm của con xúc xắc là số chia hết cho 2"
Không gian mẫu \(\Omega=\left\{S;N;1;2;3;4;5;6\right\}\)
\(\Rightarrow n\left(\Omega\right)=8\)
\(A=\left\{S;2;4;6\right\}\)
\(\Rightarrow n\left(A\right)=4\)
Xác suất của biến cố \(A\) :
\(P\left(A\right)=\dfrac{n\left(A\right)}{n\left(\Omega\right)}=\dfrac{4}{8}=\dfrac{1}{2}\)
Đúng 2
Bình luận (0)
Chọn ngẫu nhiên một số nguyên dương không lớn hơn 22.
a) Mô tả không gian mẫu.
b) Gọi B là biến cố: “Số được chọn chia hết cho 3". Các biến cố B và \(\overline B \) là các tập con nào của không gian mẫu?
a) Ta có \(\Omega = \left\{ {1;2;...;22} \right\}\).
b) \(B = \left\{ {3;6;9;12;15;18;21} \right\}\).
\(\overline A = \left\{ {1;2;4;5;7;8;10;11;13;14;16;17;19;20;22} \right\}\).
Đúng 0
Bình luận (0)