Để tính ∫ x ln ( 2 + x ) d x theo phương pháp tính nguyên hàm từng phần, ta đặt:
A. u = v d v = ln 2 + x d x
B. u = ln 2 + x d v = x d x
C. u = x ln 2 + x d v = d x
D. u = ln 2 + x d v = d x
PB
Những câu hỏi liên quan
Để tính
∫
xln
(
2
+
x
)
.
dx
theo phương pháp tính nguyên hàm từng phần, ta đặt: A.
u
v
d
v
ln
2...
Đọc tiếp
Để tính ∫ xln ( 2 + x ) . dx theo phương pháp tính nguyên hàm từng phần, ta đặt:
A. u = v d v = ln 2 + x d x
B. u = ln 2 + x d v = x d x
C. u = x ln 2 + x d v = d x
D. u = ln 2 + x d v = d x
Chọn B.
Chú ý: “ Nhất log, nhì đa, tam lượng, tứ mũ”.
Đúng 0
Bình luận (0)
Để tính
∫
x
2
.
cos
x
.
d
x
theo phương pháp tính nguyên hàm từng phần, ta đặt: A.
u
x
d
v
x
cos
x
d...
Đọc tiếp
Để tính ∫ x 2 . cos x . d x theo phương pháp tính nguyên hàm từng phần, ta đặt:
A. u = x d v = x cos x d x
B. u = x 2 d v = cos x d x
C. u = cos x d v = x 2 d x
D. u = x 2 cos x d v = d x
Chọn B.
Chú ý: “ Nhất log, nhì đa, tam lượng, tứ mũ”.
Đúng 0
Bình luận (0)
Hãy tính ∫ x + 1 e x d x bằng phương pháp tính nguyên hàm từng phần.
Áp dụng phương pháp tính nguyên hàm từng phần, hãy tính: ∫ x ln ( 1 - x ) d x
x 2 2 ln 1 - x - 1 2 ln 1 - x - 1 4 1 + x 2 + C
Đúng 0
Bình luận (0)
Sử dụng phương pháp tính nguyên hàm từng phần, hãy tính :
a) \(\int x\ln\left(1+x\right)dx\)
b) \(\int\left(x^2+2x-1\right)e^xdx\)
c) \(\int x\sin\left(2x+1\right)dx\)
d) \(\int\left(1-x\right)\cos xdx\)
a) Áp dụng phương pháp tìm nguyên hàm từng phần:
Đặt u= ln(1+x)
dv= xdx
=> ,
Ta có: ∫xln(1+x)dx =
=
b) Cách 1: Tìm nguyên hàm từng phần hai lần:
Đặt u= (x2+2x -1) và dv=exdx
Suy ra du = (2x+2)dx, v = ex
. Khi đó:
∫(x2+2x - 1)exdx = (x2+2x - 1)exdx - ∫(2x+2)exdx
Đặt : u=2x+2; dv=exdx
=> du = 2dx ;v=ex
Khi đó:∫(2x+2)exdx = (2x+2)ex - 2∫exdx = ex(2x+2) – 2ex+C
Vậy
∫(x2+2x+1)exdx = ex(x2-1) + C
Cách 2: HD: Ta tìm ∫(x2-1)exdx. Đặt u = x2-1 và dv=exdx.
Đáp số : ex(x2-1) + C
c) Đáp số:
HD: Đặt u=x ; dv = sin(2x+1)dx
d) Đáp số : (1-x)sinx - cosx +C.
HD: Đặt u = 1 - x ;dv = cosxdx
Đúng 0
Bình luận (0)
Áp dụng phương pháp tính nguyên hàm từng phần, hãy tính :
a) intleft(1-2xright)e^xdx
b) int xe^{-x}dx
c) int xlnleft(1-xright)dx
d) int xsin^2xdx
e) intlnleft(x+sqrt{1+x^2}right)dx
g) intsqrt{x}ln^2xdx
h) int xlndfrac{1+x}{1-x}dx
Đọc tiếp
Áp dụng phương pháp tính nguyên hàm từng phần, hãy tính :
a) \(\int\left(1-2x\right)e^xdx\)
b) \(\int xe^{-x}dx\)
c) \(\int x\ln\left(1-x\right)dx\)
d) \(\int x\sin^2xdx\)
e) \(\int\ln\left(x+\sqrt{1+x^2}\right)dx\)
g) \(\int\sqrt{x}\ln^2xdx\)
h) \(\int x\ln\dfrac{1+x}{1-x}dx\)
a) Phát biểu định nghĩa nguyên hàm của hàm số \(f\left(x\right)\) trên một khoảng
b) Nêu phương pháp tính nguyên hàm từng phần. Cho ví dụ minh họa
Áp dụng phương pháp tính nguyên hàm từng phần, hãy tính:
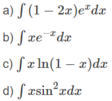
Áp dụng phương pháp tính nguyên hàm từng phần, hãy tính: ∫ x sin 2 x d x
x 2 4 - x 4 sin 2 x - 1 8 c o s 2 x + C
HD: Đặt u = x, dv = sin 2 x dx
Đúng 0
Bình luận (0)