Số phức z thay đổi thỏa mãn:|z-3+4i| = 2. Tính Min z ¯ .
A. Min z ¯ = 2
B. Min z ¯ = 3
C. Min z ¯ = 4
D. Min z ¯ = 1
Cho số phức z thay đổi thỏa mãn z - 3 - 4 i ≤ 2 Đặt w = z - 2 2 - 2 i + 1 tập hợp tất cả các điểm biểu diễn số phức w là một hình tròn có diện tích bằng
![]()
![]()
![]()
![]()
Cho số phức z thay đổi thỏa mãn z - 3 - 4 i ≤ 2 . Đặt w=(z-2)(2-2i)+1, tập hợp tất cả các điểm biểu diễn số phức w là một hình tròn có diện tích bằng
A. 8 π
B. 12 π
C. 16 π
D. 32 π
Cho số phức z thỏa mãn z 2 - 2 z + 5 = ( z - 1 + 2 i ) ( z + 3 i - 1 ) .Tính min |w|, với w = z - 2 + 2 i
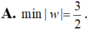
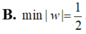
![]()
![]()
Biết các số phức z thỏa mãn : |z+1| + |z-1| = 4. Tìm Min |z|
A. z m i n = 3
B. z m i n = 1
C. z m i n = 2 - 1
D. z m i n = 2
Cho các số phức z thỏa mãn |z2 + 4| = 2|z|. Kí hiệu M = max|z| và m = min|z|. Tìm module của số phức w = M + m?
![]()
![]()
![]()
![]()
Chọn A.
Ta có ![]()
Giải bất phương trình trên với ẩn |z| ta được:
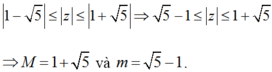
Vậy ![]()
Cho hai số phức \(z\) và \(w\) thay đổi thỏa mãn các điều kiện \(\left|z+1+i\right|=\left|z\right|\) và \(\left|w-3-4i\right|=1\). Tìm giá trị nhỏ nhất của biểu thức \(P=\left|z-w-1-i\right|\)
A.\(minP=5\sqrt{2}\) B. \(minP=5\sqrt{2}-1\) C. \(minP=3\sqrt{2}\) D. \(minP=3\sqrt{2}-1\)
Mình cần bài giải ạ, mình cảm ơn nhiều♥

\(z=x+yi\Rightarrow\left(x+1\right)^2+\left(y+1\right)^2=x^2+y^2\)
\(\Rightarrow x+y+1=0\Rightarrow\) tập hợp z là đường thẳng d: \(x+y+1=0\)
\(P=\left|\left(z-4-5i\right)-\left(w-3-4i\right)\right|\ge\left|\left|z-4-5i\right|-\left|w-3-4i\right|\right|=\left|\left|z-4-5i\right|-1\right|\)
Gọi M là điểm biểu diễn z và \(A\left(4;5\right)\Rightarrow\left|z-4-5i\right|=AM\)
\(AM_{min}=d\left(A;d\right)=\dfrac{\left|4+5+1\right|}{\sqrt{1^2+1^2}}=5\sqrt{2}\)
\(\Rightarrow P\ge\left|5\sqrt{2}-1\right|=5\sqrt{2}-1\)
Biết số phức z thỏa mãn đồng thời hai điều kiện z - 3 - 4 i = 5 và biểu thức M = | z + 2 | 2 - | z - i | 2 đạt giá tri lớn nhất. Tính môđun của số phức z+i
![]()
![]()
![]()
![]()
Biết các số phức z thỏa mãn |z-3|=|z+4i|. Tìm w m i n biết w = z + 4i -3
A. w m i n = 7 5
B. w m i n = 7 10
C. w m i n = 7 12
D. w m i n = 7
Cho số phức z thỏa mãn |z - 2 + 3i| + |z - 2 + i| = 4 5 . Tính GTLN của P = |z - 4 + 4i|
A. maxP = 4 5
B. maxP = 7 5
C. maxP = 5 5
D. maxP = 6 5
Đáp án A
Cho số phức z = x + yi (x,y ∈ R) , S(x,y) là điểm biểu diễn của z trên hệ trục tọa độ Oxy
![]()
![]()
Lấy các điểm A(2; - 3), B( - 2; - 1)
Phương trình
![]()
=> Tập hợp các điểm S là đường elip (E) có tiêu điểm A(2;
-
3), B(
-
2;
-
1) và có độ dài trục lớn là ![]()
Lấy M(4;
-
4). Dễ dàng kiểm tra được 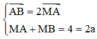
Suy ra, M là một đỉnh và nằm trên trục lớn của elip (E).
Gọi I là trung điểm AB => I(0;
-
2), N là điểm đối xứng của M qua I. Khi đó, với mọi điểm ![]()
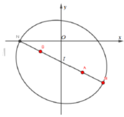
![]() khi và chỉ khi S trùng N
khi và chỉ khi S trùng N ![]() khi và chỉ khi
khi và chỉ khi ![]()