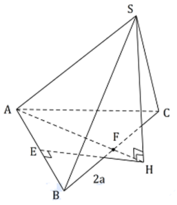
Cho hình chóp S.ABC có SA = SB = SC = a 2 và đáy là tam giác ABC cân tại A. Biết ACB ^ = 60 o và BC = 2a. Thể tích khối chóp S.ABC là
A. a 3 2 6
B. a 3 3 9
C. a 3 2 9
D. a 3 2 3
PB
Những câu hỏi liên quan
Cho hình chóp S.ABC có
SA
SB
SC
a
2
và đáy là tam giác ABC cân tại A. Biết
BAC
120
°
và BC 2a. Thể tích khối chóp S.ABC là A.
a
3
2
6...
Đọc tiếp
Cho hình chóp S.ABC có SA = SB = SC = a 2 và đáy là tam giác ABC cân tại A. Biết BAC = 120 ° và BC = 2a. Thể tích khối chóp S.ABC là
A. a 3 2 6 .
B. a 3 3 9 .
C. a 3 2 9 .
D. a 3 2 3 .
Đáp án C
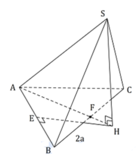
Gọi H là tâm đường tròn ngoại tiếp tam giác ABC bằng cách dựng như hình vẽ.
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A,
AB
a
2
,
SA
SB
SC
. Góc giữa SA và mặt phẳng (ABC) bằng
60
0
. Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABC theo a. A.
2
a
3
B.
a...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, AB = a 2 , SA = SB = SC . Góc giữa SA và mặt phẳng (ABC) bằng 60 0 . Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABC theo a.
A. 2 a 3
B. a 3 2
C. 2 a 3 5
D. 2 a 3
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, cạnh bên SA vuông góc với đáy. Biết BA=a, SC= a căn 3. Góc giữa SB và (SAC)
Xem chi tiết
Gọi M là trung điểm AC \(\Rightarrow BM\perp AC\)
\(\Rightarrow BM\perp\left(SAC\right)\Rightarrow\widehat{BSM}\) là góc giữa SB và (SAC)
\(AC=a\sqrt{2}\) ; \(AM=BM=\dfrac{AC}{2}=\dfrac{a\sqrt{2}}{2}\)
\(SA=\sqrt{SC^2-AC^2}=a\Rightarrow SB=a\sqrt{2}\)
\(sin\widehat{BSM}=\dfrac{BM}{SB}=\dfrac{1}{2}\Rightarrow\widehat{BSM}=30^0\)
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A , mặt phẳng (SBC) vuông góc với mặt phẳng (ABC) và SASBABACa; SCa
2
. Diện tích xung quanh mặt cầu ngoại tiếp hình chóp S.ABC bằng: A. 2
πa
2
B.
πa
2
C. 8
πa
2
D. 4
πa
2
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A , mặt phẳng (SBC) vuông góc với mặt phẳng (ABC) và SA=SB=AB=AC=a; SC=a 2 . Diện tích xung quanh mặt cầu ngoại tiếp hình chóp S.ABC bằng:
A. 2 πa 2
B. πa 2
C. 8 πa 2
D. 4 πa 2
Cho hình chóp S.ABC có SASASCa
2
và đáy là tam giác ABC cân tại A. Biết góc BAC
120
o
và BC 2a. Thể tích khối chóp S.ABC là A
.
a
3
2
6
B
.
a
3
3...
Đọc tiếp
Cho hình chóp S.ABC có SA=SA=SC=a 2 và đáy là tam giác ABC cân tại A. Biết góc BAC= 120 o và BC = 2a. Thể tích khối chóp S.ABC là
A . a 3 2 6
B . a 3 3 9
C . a 3 2 9
D . a 3 2 3
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân, ABACa, SC
⊥
(ABC) và SCa. Mặt phẳng qua C vuông góc với SB cắt SA SB , lần lượt tại E, F. Tính thể tích khối chóp S.CEF A.
V
S
.
C
E
F
2
a
3
36
B.
V...
Đọc tiếp
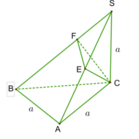
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân, AB=AC=a, SC ⊥ (ABC) và SC=a. Mặt phẳng qua C vuông góc với SB cắt SA SB , lần lượt tại E, F. Tính thể tích khối chóp S.CEF
A. V S . C E F = 2 a 3 36
B. V S . C E F = a 3 36
C. V S . C E F = a 3 18
D. V S . C E F = 2 a 3 12
Cho hình chóp S. ABC có đáy ABC là tam giác cân tại A, biết AB a; SA SB a và mặt phẳng (SBC) vuông góc với mặt phẳng (ABC). Tính SC biết bán kính mặt cầu ngoại tiếp hình chóp S.ABC bằng a. A.
S
C
a
3
B.
S
C
a
2
C.
S
C
a
D.
S
C
a
2...
Đọc tiếp
Cho hình chóp S. ABC có đáy ABC là tam giác cân tại A, biết AB = a; SA = SB = a và mặt phẳng (SBC) vuông góc với mặt phẳng (ABC). Tính SC biết bán kính mặt cầu ngoại tiếp hình chóp S.ABC bằng a.
A. S C = a 3
B. S C = a 2
C. S C = a
D. S C = a 2 2
Chọn B.
Phương pháp:
+ Gọi H là trung điểm BC. Ta chứng minh A H ⊥ A B C và AH là trục đường tròn ngoại tiếp tam giác
SBC
+ Suy ra tâm mặt cầu ngoại tiếp chóp S. ABC là giao của AH và đường trung trực cạnh AB.
+ Chỉ ra tam giác SBC vuông tại S từ đó tính SC theo định lý Pytago.
Cách giải:
Đúng 0
Bình luận (0)
Cho hình chóp S. ABC có đáy ABC là tam giác cân tại A, biết AB a; SA SB a và mặt phẳng (SBC) vuông góc với mặt phẳng (ABC). Tính SC biết bán kính mặt cầu ngoại tiếp hình chóp S.ABC bằng a.
Đọc tiếp
Cho hình chóp S. ABC có đáy ABC là tam giác cân tại A, biết AB = a; SA = SB = a và mặt phẳng (SBC) vuông góc với mặt phẳng (ABC). Tính SC biết bán kính mặt cầu ngoại tiếp hình chóp S.ABC bằng a.
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B với ACa, biết SA vuông góc với đáy ABC và SB hợp với đáy một góc
60
°
. Tính thể tích hình chóp A.
a
3
3
12
B.
a
3
6...
Đọc tiếp
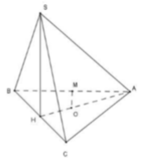
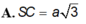
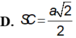
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B với AC=a, biết SA vuông góc với đáy ABC và SB hợp với đáy một góc 60 ° . Tính thể tích hình chóp
A. a 3 3 12
B. a 3 6 24
C. 2 a 3 3
D. 3 a 3 2
