Số nghiệm thực của phương trình 4 x - 1 + 2 x + 3 - 4 = 0 là
A. 1
B. 2
C. 3
D. 0
Số nghiệm thực của phương trình (x - 4) (√3-x-1) = 0
A.0 B.1 C.2 D.4
Lời giải:
ĐKXĐ: $x\leq 3$
$(x-4)(\sqrt{3-x}-1)=0$
\(\Leftrightarrow \left[\begin{matrix} x-4=0\\ \sqrt{3-x}-1=0\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x=4(\text{loại do 4>3})\\ x=2(tm)\end{matrix}\right.\)
Vậy số nghiệm thực của pt là $1$
Đáp án B.
Cho số thức α sao cho phương trình 2 x - 2 - x = 2 cos α x có đúng 2019 nghiệm thực. Số nghiệm của phương trình 2 x + 2 - x = 4 + 2 cos α x là:
A. 2019
B. 2018
C. 4037
D. 4038
Cho phương trình ( x + x + 1 ) ( m x + 1 + 1 x + 16 x 2 + x 4 ) = 1 với m là tham số thực. Tìm số các giá trị nguyên của m để phương trình có hai nghiệm thực phân biệt
A. 3.
B. 4.
C. 5.
D. 6
Số các giá trị thực của tham số m để phương trình (sin x-1)(2cos^2 x - (sinx -1)(2 cos 2 x –(2m+1)cosx+m)=0 có đúng 4 nghiệm thực thuộc đoạn 0 ; 2 π là
A. 1.
B. 2.
C. 3.
D. Vô số.
Đáp án B.
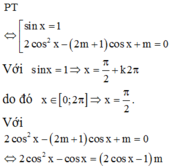
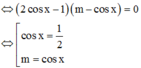
PT: cos x = 1 2 có 2 nghiệm thuộc trên đoạn 0 ; 2 π do đó để PT đã cho có 4 nghiệm thực thuộc đoạn 0 ; 2 π thì
TH1: m= cosx có 1 nghiệm thuộc đoạn 0 ; 2 π
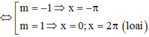
TH2: m= cosx có 2 nghiệm thuộc đoạn 0 ; 2 π trong đó có 1 nghiệm trùng
![]()
Vậy m= -1; m=0.
Cho tham số thực a. Biết phương trình ex - e-x = 2 cosax có 5 nghiệm thực phân biệt. Hỏi phương trình ex - e-x = 2 cosax + 4 có bao nhiêu nghiệm thực phân biệt?
A. 5.
B. 6.
C. 10.
D. 11.
Chọn C.
Ta có
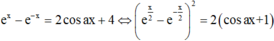
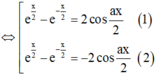
Giả sử x0 là nghiệm của phương trình ex - e-x = 2 cosax (*), thì x0 ≠ 0 và 2x0 là nghiệm của (1) và -2x0 là nghiệm của (2) hoặc ngược lại
Phương trình (*) có 5 nghiệm nên hai phương trình (1), (2) có 5 nghiệm phân biệt.
Vậy phương trình ex - e-x = 2 cosax + 4 có 10 nghiệm phân biệt.
Số nghiệm thực của phương trình \(x^4-9x^2+24x-16=0\)
\(\Leftrightarrow x^4-x^3+x^3-x^2-8x^2+8x+16x-16=0\\ \Leftrightarrow\left(x-1\right)\left(x^3+x^2-8x+16\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x^3+4x^2-3x^2-12x+4x+16\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x+4\right)\left(x^2-3x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=-4\\\left(x-\dfrac{3}{2}\right)^2+\dfrac{7}{4}=0\left(vô.n_o\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-4\end{matrix}\right.\)
1) Tìm các tham số thực $m$ để phương trình $9 x^{2}-m x+1=0$ có nghiệm kép.
2) Cho $x_{1}$ và $x_{2}$ là hai nghiệm của phương trình $x^{2}-2 x-4=0$. Tính giá trị của biểu thức $T=x_{1}\left(x_{1}-2 x_{2}\right)+x_{2}\left(x_{2}-2 x_{1}\right)$.
Bài 2 :
Theo Vi et ta có : \(\hept{\begin{cases}x_1+x_2=-\frac{b}{a}=2\\x_1x_2=\frac{c}{a}=-4\end{cases}}\)
mà \(\left(x_1+x_2\right)^2=4\Rightarrow x_1^2+x_2^2=4+8=12\)
Ta có : \(T=x_1\left(x_1-2x_2\right)+x_2\left(x_2-2x_1\right)\)
\(=x_1^2-2x_2x_1+x_2^2-2x_1x_2=12+16=28\)
Tìm tất cả các giá trị thực của m để phương trình \(4^x-2^{x+1}+m=0\) có 2 nghiệm thực phân biệt
Đặt \(t=2^x>0\).
Phương trình ban đầu trở thành: \(t^2-2t+m=0\) (*)
Để phương trình ban đầu có 2 nghiệm phân biệt thì (*) phải có 2 nghiệm phân biệt dương: \(\left\{{}\begin{matrix}\Delta'>0\\t_1+t_2>0\\t_1t_2>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}1-m>0\\2>0\left(đúng\right)\\m>0\end{matrix}\right.\Leftrightarrow0< m< 1\)
Tổng bình phương các nghiệm của phương trình \(x^3+1=2\sqrt[3]{x^2+5x-2}-2\) trên tập số thực bằng
Em kiểm tra lại đề bài, pt này chắc chắn là ko giải được
Cho tham số thực a. Biết phương trình e x - e - x = 2 cos a x có 5 nghiệm thực phân biệt. Hỏi phương trình e x - e - x = 2 cos a x + 4 có bao nhiêu nghiệm thực phân biệt?
A. 5.
B. 6.
C. 10.
D. 11.