Cho hệ phương trình 8 x + 7 y = 16 8 x - 3 y = - 24 . Nghiệm của hệ phương trình là
A. x ; y = - 3 2 ; 4
B. x ; y = 4 ; - 3 2
C. x ; y = - 3 2 ; - 4
D. x ; y = - 2 ; 2
Giải hệ phương trình: (x+y)(x+z)= 8 và (y+x)(y+z)=16 và (z+x)(z+y)=32
\(\hept{\begin{cases}\left(x+y\right)\left(x+z\right)=8\left(1\right)\\\left(x+y\right)\left(y+z\right)=16\left(2\right)\\\left(x+z\right)\left(z+y\right)=32\left(3\right)\end{cases}}\)
Nhân các phương trình (1) , (2) , (3) theo vế ta được : \(\left[\left(x+y\right)\left(y+z\right)\left(x+z\right)\right]^2=4096\Rightarrow\left(x+y\right)\left(y+z\right)\left(x+z\right)=64\)hoặc \(\left(x+y\right)\left(y+z\right)\left(z+x\right)=-64\)
1. Với (x+y)(y+z)(z+x) = 64 , từ (1) , (2) , (3) suy ra \(\hept{\begin{cases}x+y=2\\y+z=8\\z+x=4\end{cases}\Leftrightarrow}\hept{\begin{cases}x=-1\\y=3\\z=5\end{cases}}\)
2. Với (x+y)(y+z)(z+x) = -64 , từ (1) , (2) , (3) suy ra : \(\hept{\begin{cases}x+y=-2\\y+z=-8\\z+x=-4\end{cases}\Leftrightarrow\hept{\begin{cases}x=1\\y=-3\\z=-5\end{cases}}}\)
Vậy nghiệm của hệ là : \(\left(x;y;z\right)=\left(-1;3;5\right);\left(1;-3;-5\right)\)
cho hệ phương trình\(\hept{\begin{cases}3x-my=-9\\mx+2y=16\end{cases}}\)
a) giải hệ phương trình khi m = 5
b) chứng tỏ rằng hệ phương trình luôn luôn có nghiệm duy nhất với mọi m
c) định m để hệ có nghiệm (x ; y) = (1,4 ; 6,6)
d) với trị nguyên nào của m để hệ có nghiệm (x ; y) thỏa mãn x + y = 7
giúp mình với mình cần nộp trong ngày 17/2/2020
Giải mấy bài này mệt ghê ~
a,Thay m = 5 vào PT \(\hept{\begin{cases}3x-my=-9\\mx+2y=16\end{cases}}\)
\(< =>\hept{\begin{cases}3x-5y=-9\\5x+2y=16\end{cases}}\)
\(< =>\hept{\begin{cases}15x-25y=-45\\15x+6y=48\end{cases}}\)
\(< =>\hept{\begin{cases}31y=93\\3x-5y=-9\end{cases}}\)
\(< =>\hept{\begin{cases}y=3\\3x=6\end{cases}}\)
\(< =>\hept{\begin{cases}y=3\\x=2\end{cases}}\)
b,Ta thay : \(\hept{\begin{cases}y=3\\x=2\end{cases}}\)vào PT ta đc :
\(\hept{\begin{cases}6-3m=-9\\2m+6=16\end{cases}}\)
\(< =>\hept{\begin{cases}m=5\\m=5\end{cases}}\)(đề sai ? hay do mk ngu ?)
c,bạn thay nghiệm vào là đc nhé <3
Giải hệ phương trình :
\(\hept{\begin{cases}x+y+z=16\\\sqrt{x+y}+\sqrt{y+z}+\sqrt{z+x}=8\end{cases}}\)
\(\hept{\begin{cases}\left(x+y\right)+\left(y+z\right)+\left(z+x\right)=32\\\sqrt{x+y}+\sqrt{y+z}+\sqrt{z+x}=8\end{cases}\Leftrightarrow\hept{\begin{cases}a^2+b^2+c^2=32\\a+b+c=8\end{cases}}}\)
\(a^2+b^2+c^2=2a+2b+2c\Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0.\)
\(\Rightarrow a=b=c\)
\(\Leftrightarrow x=y=z=\frac{16}{3}\)
uk. sai rồi
Bạn giúp mình đi.
Giải hệ phương trình sau bằng phương pháp thế (biểu diễn y theo x từ phương trình thứ hai của hệ)
4 x − 5 y = 3 3 x − y = 16
Ta có ( biểu diễn y theo x từ phương trình thứ hai):
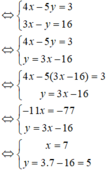
Vậy hệ phương trình có nghiệm duy nhất (7;5)
Giải hệ phương trình sau bằng phương pháp thế (biểu diễn y theo x từ phương trình thứ hai của hệ) 4 x - 5 y = 3 3 x - y = 16
Ta có ( biểu diễn y theo x từ phương trình thứ hai):
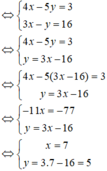
Vậy hệ phương trình có nghiệm duy nhất (7;5)
Câu 1:
1. Thực hiện phép tính: \(16\sqrt{9}-9\sqrt{16}\)
2. Cho hàm số y = ax\(^2\) với a là tham số
a) Tìm a để đồ thị hàm số qua điểm M (2; 8)
b) Vẽ đồ thị của hàm số ứng với giá trị a tìm được
Câu 2:
1. Giải phương trình và hệ phương trình sau:
a) x\(^2\) - 5x + 4 = 0
b) \(\left\{{}\begin{matrix}3x+2y=8\\2x-y=3\end{matrix}\right.\)
2. Cho phương trình x - 2 (m + 1)x + m - 4 = 0
a) Chứng minh rằng phương trình luôn có hai nghiệm phân biệt với mọi m
b) Gọi x\(_1\), x\(_2\) là hai nghiệm của phương trình đã cho. Chứng minh giá trị biểu thức A = x\(_1\)(1 - x\(_2\)) + x\(_2\) (1 - x\(_1\)) không phụ thuộc m
Câu 1:
1: Ta có: \(16\sqrt{9}-9\sqrt{16}\)
\(=16\cdot3-9\cdot4\)
\(=48-36=12\)
2:
a) Thay x=2 và y=8 vào hàm số \(y=a\cdot x^2\), ta được:
\(a\cdot2^2=8\)
\(\Leftrightarrow4a=8\)
hay a=2
Vậy: a=2
Câu 2:
1:
a) Ta có: \(x^2-5x+4=0\)
\(\Leftrightarrow x^2-x-4x+4=0\)
\(\Leftrightarrow x\left(x-1\right)-4\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=4\end{matrix}\right.\)
Vậy: S={1;4}
Cho hệ phương trình 2 x - 3 y + 4 z = - 5 - 4 x + 5 y - z = 6 3 x + 4 y - 3 z = 7 . Giả sử (x;y;z) là nghiệm của hệ phương trình, khi đó x+y+z bằng
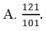
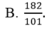
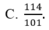
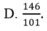
cho hệ phương trình mx+2y=1
2x-4y=3
tìm m để hệ phương trình có nghiệm duy nhất (x;y) thỏa mãn x-3y=7/2
Để hệ phương trình có nghiệm duy nhất thì \(\dfrac{m}{2}\ne\dfrac{2}{-4}=-\dfrac{1}{2}\)
=>\(m\ne-1\)
\(\left\{{}\begin{matrix}mx+2y=1\\2x-4y=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2mx+4y=2\\2x-4y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\left(2m+2\right)=5\\2x-4y=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{5}{2m+2}\\4y=2x-3=\dfrac{10}{2m+2}-3=\dfrac{10-6m-6}{2m+2}=\dfrac{-6m+4}{2m+2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{5}{2m+2}\\y=\dfrac{-6m+4}{8m+8}=\dfrac{-3m+2}{4m+4}\end{matrix}\right.\)
x-3y=7/2
=>\(\dfrac{5}{2m+2}-\dfrac{3\cdot\left(-3m+2\right)}{4m+4}=\dfrac{7}{2}\)
=>\(\dfrac{10+3\left(3m-2\right)}{4m+4}=\dfrac{7}{2}\)
=>\(\dfrac{10+9m-6}{4m+4}=\dfrac{7}{2}\)
=>\(\dfrac{9m+4}{4m+4}=\dfrac{7}{2}\)
=>7(4m+4)=2(9m+4)
=>28m+28=18m+8
=>10m=-20
=>m=-2(nhận)
Giải hệ phương trình
(x+3) (y+5) = (x+1) (y+8)
(2x-3) (5y+7) = 2((5x-6) (y+1)
<=> xy+5x+3y+15=xy+8x+y+8 <=> 3x-2y=7 <=> 9x-6y=21 <=> x=3 <=> x=3
10xy+14x-15y-21=10xy+10x-12y-12 4x-3y=9 8x-6y=18 8.3-6y=18 y=1
Giải hệ phương trình
(x+3) (y+5) = (x+1) (y+8)
(2x-3) (5y+7) = 2((5x-6) (y+1)
em moi hoc lop 6 thoi sao lam duoc toan lop 9