Tập nghiệm S của phương trình log 2 x + 4 = 4 là:
A. S = − 4 , 12 .
B. S = 4 .
C. S = 4 , 8 .
Tập nghiệm của bất phương trình
log ( x 2 - 4 ) > log ( 3 x ) là:
![]()
![]()
![]()
![]()
Biết rằng tập nghiệm S của bất phương trình log - x 2 + 100 x - 2400 < 2 có dạng S = a ; b \ x ∘ . Giá trị của a + b - x ∘ bằng:
A. 150.
B. 100.
C. 30.
D. 50.
Tập nghiệm của bất phương trình log 2 x - 1 ≥ log x là
![]()
![]()
![]()
![]()
Câu 3. Phương trình vô nghiệm có tập nghiệm là?
A. S = f B. S = 0 C. S = {0} D. S = {f}
Câu 4. Điều kiện xác định của phương trình là?
A. x ≠ 2 và B. x ≠ -2 và C. x ≠ -2 và x ≠ 3 D. x ≠ 2 và
Câu 5. Cho AB = 3cm, CD = 40cm. Tỉ số của hai đoạn thẳng AB và CD bằng?
A. B. C. D.
Biết rằng tập nghiệm S của bất phương trình log - x 2 + 100 x - 2400 < 2 có dạng S = a ; b \ x 0 . Giá trị của a + b - x 0 bằng:
A. 100
B. 30
C. 150
D. 50
Biết rằng tập nghiệm S của bất phương trình log - x 2 + 100 x - 2400 < 2 có dạng S = (a;b)\{x0}. Giá trị của a + b – x0 bằng:
A. 100
B. 30
C. 150
D. 50
Đáp án D.
Phương pháp: ![]()
Cách giải: ĐK: ![]()
![]()
![]()
![]()
![]()
![]()
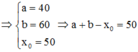
Tập nghiệm của bất phương trình \({\log _{\frac{1}{4}}}x > - 2\) là:
A. \(\left( { - \infty ;16} \right)\)
B. \(\left( {16; + \infty } \right)\)
C. \((0;16)\)
D. \(\left( { - \infty ;0} \right)\)
\(\log_{\dfrac{1}{4}}x>-2\\ \Rightarrow\left\{{}\begin{matrix}x>0\\\log_{\dfrac{1}{4}}x>\log_{\dfrac{1}{4}}16\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x>0\\x< 16\end{matrix}\right.\\ \Leftrightarrow0< x< 16\)
Chọn C.
Tập nghiệm của bất phương trình log(x2 + 25) > log(10x) là
![]()
![]()
![]()
![]()
Gọi S là tập nghiệm của bất phương trình \(\dfrac{x^2+x+3}{x^2-4}\ge1\) . Khi đó S \(\cap\left(-2;2\right)\) là tập nghiệm nào
\(\dfrac{x^2+x+3}{x^2-4}\ge1\Leftrightarrow\dfrac{x^2+x+3}{x^2-4}-1\ge0\)
\(\Leftrightarrow\dfrac{x+7}{x^2-4}\ge0\Rightarrow\left[{}\begin{matrix}-7\le x< -2\\x>2\end{matrix}\right.\)
\(\Rightarrow S\cap\left(-2;2\right)=\varnothing\)
Cho phương trình log2(10x) - 2mlog10xx - log(10x2)=0 . Gọi S là tập chứa tất cả các giá trị nguyên của m thuộc [-10;10] để phương trình đã cho có đúng 3 nghiệm phân biệt . Số phần tử của tập S là